

第10回 ダミー変数
![]()
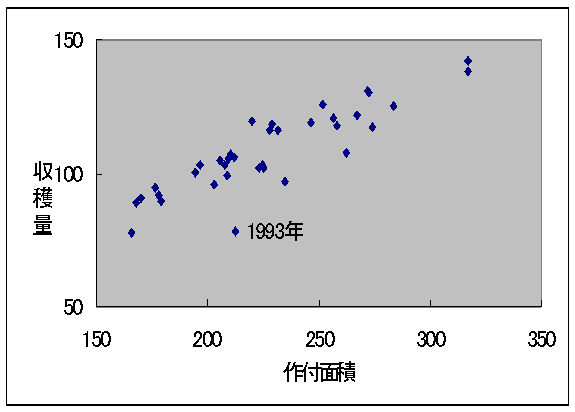
(P146)表1は、わが国の水稲の収穫量Yと作付面積Xの推移を、1985年から95年の11年間について示したものです。
(1)ヨコ軸にX、タテ軸にYをとり、このデータの散布図を描きなさい。
(2) つぎの単純回帰モデルをOLSにより推定し、t値、P値と決定係数![]() も計算しなさい。
も計算しなさい。
![]()
(3) 1993年は記録的な冷害にみまわれ、水稲の作況指数は戦後最悪(74)、未曾有の不作の年となりました。そこで、1993年をD=1、その他の年をD=0とする一時的ダミー変数を導入した、つぎの重回帰モデルを推定しなさい。t値、P値と自由度調整済決定係数![]() もあわせて計算しなさい。
もあわせて計算しなさい。
![]()
(4) (2)と(3)を比較して以下の質問に答えなさい。
①どちらのモデルが当てはまりがよいと思われますか?またその理由を答えなさい。
②ダミー変数を導入した効果はあったと思いますか?またその理由を答えなさい。
![]()
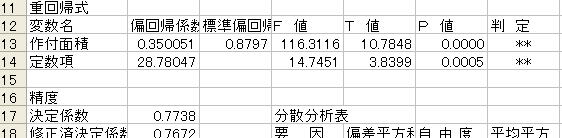
(1)、(2)は今までの復習なので結果だけ表示します。自分の結果とあっているか確認してください。
![]()
![]()
![]()
![]()
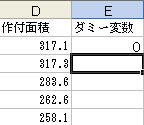
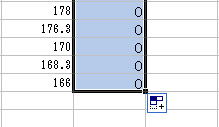
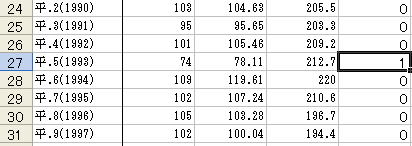
E列にダミー変数を入力して重回帰分析を行います。
ダミー変数には1993年以外は「0」、1993年には「1」と入力していきます。
まず「E1」には「ダミー変数」と入力しましょう。
また「E2」には「0」と入力しましょう。
「E2」をコピーし、1993年以外に貼り付け、1993年には「1」と入力します。
エクセル統計で重回帰分析を行います。
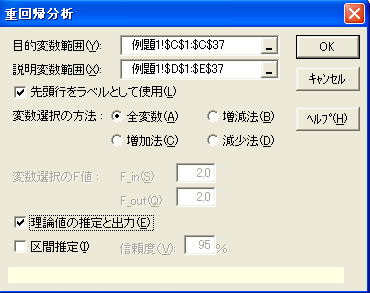
![]() 目的変数は単回帰分析と同じC列を指定します。
目的変数は単回帰分析と同じC列を指定します。
![]() 説明変数は作付面積のD列と作成したダミー変数のE列を指定します。
説明変数は作付面積のD列と作成したダミー変数のE列を指定します。
![]() 変数選択はダミー変数を用いる場合は行ってほしくはないので「全変数」とします。
変数選択はダミー変数を用いる場合は行ってほしくはないので「全変数」とします。
![]() 「OK」を押すと結果が表示されます。
「OK」を押すと結果が表示されます。
![]()
![]() (2)、(3)の結果から比較して答えます。
(2)、(3)の結果から比較して答えます。

![]() 当てはまりのよさを測るのは決定係数でした。比較する場合は値が大きくなっていればあてはまりがよいといえます。この場合は重回帰分析も行っているので修正済決定係数で比較します。
当てはまりのよさを測るのは決定係数でした。比較する場合は値が大きくなっていればあてはまりがよいといえます。この場合は重回帰分析も行っているので修正済決定係数で比較します。
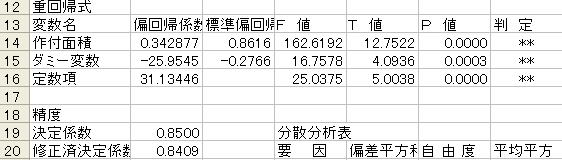
(2)と(3)では(3)のほうが決定係数の値が高いため、こちらのほうがよいモデルといえます。
![]()
(3) 理由;修正済決定係数を比較すると(2)のモデルでは0.7672、(3)では0.8409となっていて(3)のほうが高くなっているため
![]() ダミー変数を導入した効果があるかは回帰係数β2に関する仮説検定を行います。
ダミー変数を導入した効果があるかは回帰係数β2に関する仮説検定を行います。
![]()
もし帰無仮説が棄却されなければ、ダミー変数がどんな数値であろうと結果には影響されません。仮説検定の結果はT値、P値を見ます。特にP値は
| P値 | 結果 |
| 0.05以上 | 棄却されない |
| 0.01以上0.05未満 | 5%有意 |
| 0.01未満 | 1%有意 |
となります。ダミー変数のT値、P値は4.0396、0.00003となっているのでP値が0.01未満で1%有意で棄却されます。よってダミー変数を導入した効果があったといえます。
![]()
効果はある。P値が0.01未満であるため1%有意でダミー変数の説明力があると判断されたため
![]()
表2の四半期データは、わが国の食費総額(食品・飲料・煙草)Yと国内家計最終消費支出Xの推移を、実質額で示したものです。
(1) 次のモデル(マクロのエンゲル関数)を、OLSにより推定しなさい。また、t値、P値と自由度調整済決定係数![]() も計算しなさい。
も計算しなさい。
![]()
(2) 季節ダミー変数![]() (第1四半期)、
(第1四半期)、![]() (第2四半期)、
(第2四半期)、![]() (第3四半期)を導入した以下のモデルを推定しなさい。t値、P値と自由度調整済決定係数
(第3四半期)を導入した以下のモデルを推定しなさい。t値、P値と自由度調整済決定係数![]() もあわせて計算しなさい。
もあわせて計算しなさい。
![]()
(3) (2)の結果について以下の問いに答えなさい。
①どちらのモデルが当てはまりがよいと思われますか?またその理由を答えなさい。
②ダミー変数を導入した効果はあったと思いますか?またその理由を答えなさい。
![]()
![]() 結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。
結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。

![]()
![]()
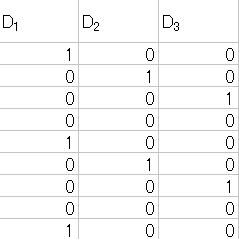
![]() まずは季節ダミー変数を作成しなければなりません。作成方法としては以下のように考えます。
まずは季節ダミー変数を作成しなければなりません。作成方法としては以下のように考えます。
| D1 | D2 | D3 | |
| 第1期 | 1 | 0 | 0 |
| 第2期 | 0 | 1 | 0 |
| 第3期 | 0 | 0 | 1 |
| 第4期 | 0 | 0 | 0 |
![]() 昭和55年のところに上の表のように数値を入力します。
昭和55年のところに上の表のように数値を入力します。
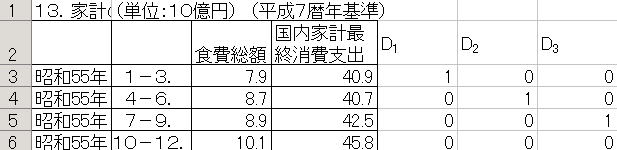
![]() 作成した昭和55年のダミー変数をコピーし、E列からG列の残りの部分に貼り付けをします。
作成した昭和55年のダミー変数をコピーし、E列からG列の残りの部分に貼り付けをします。
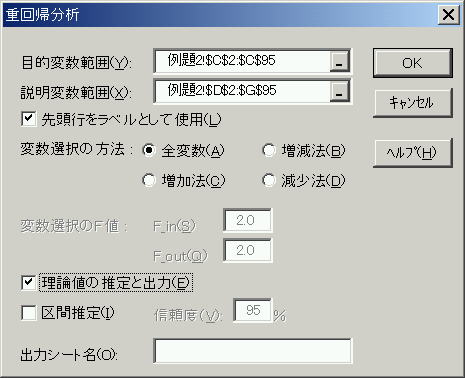
![]() 重回帰分析を行います。(変数選択は全変数)
重回帰分析を行います。(変数選択は全変数)
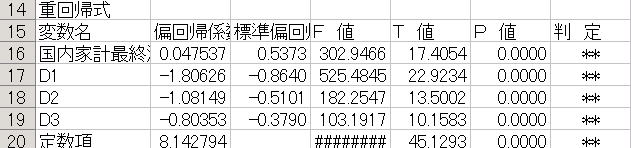
![]() 結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。
結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。
![]()
![]() ①、②は例題1と同様に答えます。
①、②は例題1と同様に答えます。
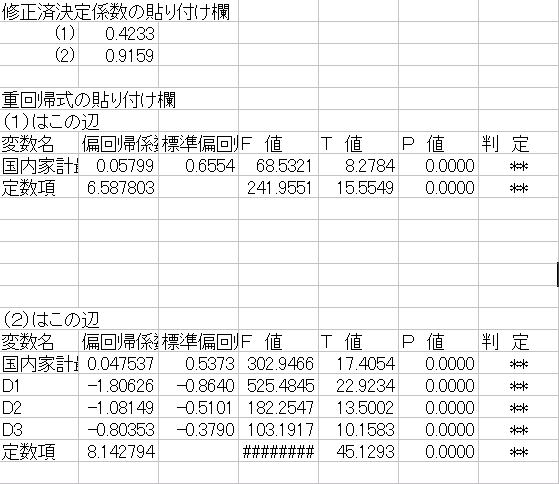
![]() (2) 理由;修正済決定係数を比較すると(1)のモデルでは0.4233、(2)では0.9159となっていて(2)のほうが高くなっているため
(2) 理由;修正済決定係数を比較すると(1)のモデルでは0.4233、(2)では0.9159となっていて(2)のほうが高くなっているため
![]() 効果はある。理由;どのダミー変数もP値が0.01未満であるため1%有意でダミー変数の説明力があると判断されたため
効果はある。理由;どのダミー変数もP値が0.01未満であるため1%有意でダミー変数の説明力があると判断されたため
![]()
![]()
表3は2000年における47都道府県における実質県民所得Y(平成7暦年価格)(10億円)と労働力人口 (千人)Xを表したものである。都道府県データを用いて労働力による生産力に関する分析を行いたい。特に労働力の大きさにより所得に影響しているのかを分析したい。そこで以下の問いに答えなさい。また、推定に関してはt値、P値と自由度調整済決定係数![]() も計算しなさい。
も計算しなさい。
(1)つぎのモデルを、OLSにより推定しなさい。
![]()
(2)政令指定都市の有無について次のダミー変数を用いて次のモデルを推定しなさい。
![]()
①定数項ダミーを導入したモデル:![]()
②係数ダミーを導入したモデル:![]()
③定数項ダミー、係数ダミーを導入したモデル:![]()
(3)(1)から(2)までの結果を見て以下の問いに答えなさい。
①どのモデルが最も当てはまりがよいと思われますか?またその理由を答えなさい。
②ダミー変数を導入した効果はあったと思いますか?またその理由を答えなさい。
![]()
![]() 結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。
結果として重要なのは以下の部分です。解答欄に以下の部分を貼り付けましょう。

![]()
![]()
![]() 政令指定都市は以下の都市があります。これに東京都を加えた12都道府県を1として残りを0とします。
政令指定都市は以下の都市があります。これに東京都を加えた12都道府県を1として残りを0とします。
| 都市名 | 都道府県名 |
| 札幌市 | 北海道 |
| 仙台市 | 宮城県 |
| さいたま市 | 埼玉県 |
| 千葉市 | 千葉県 |
| 横浜市 | 神奈川県 |
| 川崎市 | 神奈川県 |
| 名古屋市 | 愛知県 |
| 京都市 | 京都府 |
| 大阪市 | 大阪府 |
| 神戸市 | 兵庫県 |
| 広島市 | 広島県 |
| 北九州市 | 福岡県 |
| 福岡市 | 福岡県 |
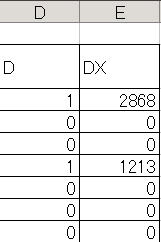
![]() 「DX」を入力するE列には「C列の値」×「D列の値」を出力されるようにします。
「DX」を入力するE列には「C列の値」×「D列の値」を出力されるようにします。
たとえば北海道の「E3」には
=C3*D3
と入力します。
この関数を他のE列にコピーすれば出来上がりです。
エクセル統計を使う場合には説明変数は隣り合っていたほうが指定しやすくできます。そこで①から③までの説明変数をまとめておきましょう。
それぞれに対して重回帰分析をおこなって結果を出力させてください。
![]() 3行目だけコピーする
3行目だけコピーする

 G列からO列まですべてにコピー
G列からO列まですべてにコピー

①の結果

![]()
②の結果

![]()
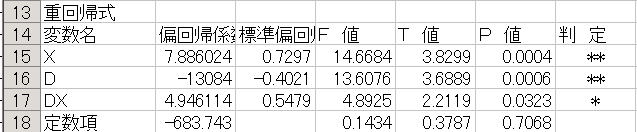
③の結果
![]()
![]()

![]() ①、②は例題1、2と同様に答えます。
①、②は例題1、2と同様に答えます。
![]() (2)の③ 理由;修正済決定係数を比較すると(2)の③が0.9050と最も高くなっているため
(2)の③ 理由;修正済決定係数を比較すると(2)の③が0.9050と最も高くなっているため
![]() 効果はある。理由;(2)③のモデルでは、ダミー変数X,DXがともに1%有意でダミー変数の説明力があると判断されたため
効果はある。理由;(2)③のモデルでは、ダミー変数X,DXがともに1%有意でダミー変数の説明力があると判断されたため
![]()
表4は1983年から2002年までの家計における可処分所得Xと消費支出Yを示しています。
(1) ヨコ軸にX、タテ軸にYをとり、このデータの散布図を描きなさい。
(2) つぎの単純回帰モデル(消費関数)をOLSにより推定し、t値、P値と決定係数![]() も計算しなさい。
も計算しなさい。
① ![]()
(3) 1993年にバブル崩壊後、日本経済は不況が続きました。特に1995年からはデフレ経済などといわれていました。このような不況により家計に構造変化があったのかを分析してみます。そこで以下のダミー変数を導入したモデルについて推定しなさい。なお、どの分析でもP値と自由度調整済決定係数![]() もあわせて計算しなさい。
もあわせて計算しなさい。
![]()
②![]()
③![]()
④![]()
(4)(2)と(3)の結果を見て以下の問いに答えなさい。
①どのモデルが最も当てはまりがよいと思われますか?またその理由を答えなさい。
②ダミー変数を導入した効果はあったと思いますか?またその理由を答えなさい。
![]()
例題3に関連して関東地方とそれ以外の地方で労働力と所得の関係が異なるかを分析したい。
(1) 関東地方とそれ以外について次のダミー変数を用いて次のモデルを推定しなさい。
① 定数ダミーを導入したモデル:
② 係数ダミーを導入したモデル:
③ 定数項ダミー、係数ダミーを導入したモデル:
(2) 関東地方とそれ以外では労働力の大きさと所得の関係の構造変化はありますか?もしあるとしたらどのような変化があるのかを述べなさい。
![]()
表5は2000年における47都道府県におけるコンビニエンススト店舗数Yと人口Xを表したものである。都道府県データを用いてコンビニ店舗数に関する分析を行いたい。そこで以下の問いに答えなさい。また、推定に関してはP値と自由度調整済決定係数![]() も計算しなさい。
も計算しなさい。
(1)つぎのモデルを、OLSにより推定しなさい。:![]()
(2)政令指定都市の有無について次のダミー変数
![]()
を用いて定数項ダミー、係数ダミーを導入したモデルを推定しなさい。
![]()
(3) ダミー変数を導入した効果はあったと思いますか?またその理由を答えなさい。