

第4回 平均値の検定と検定結果の見方

![]()
次の確率の計算を行いなさい。
|
(1) |
|
1) |
![]()
それぞれの確率を計算する場合にはEXCEL関数を用いて計算します。
EXCEL関数は
| 確率を計算する場合 | 確率点を計算する場合 | |
| 正規分布 | NORMDIST | NORMINV |
| 標準正規分布 | NORMSDIST | NORMSINV |
| t分布 | TDIST | TINV |
であらわされます。
問題によって関数を設定して引数を入力することにより求められます。
関数ダイアログボックスの例
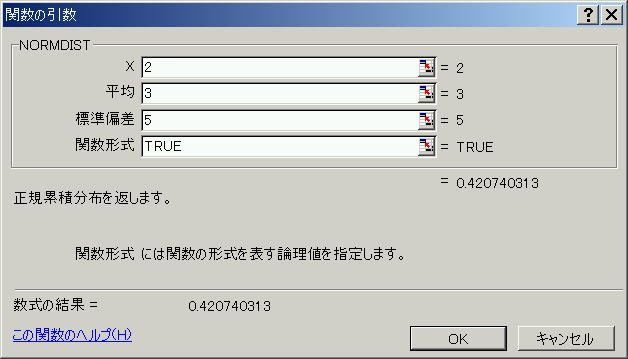
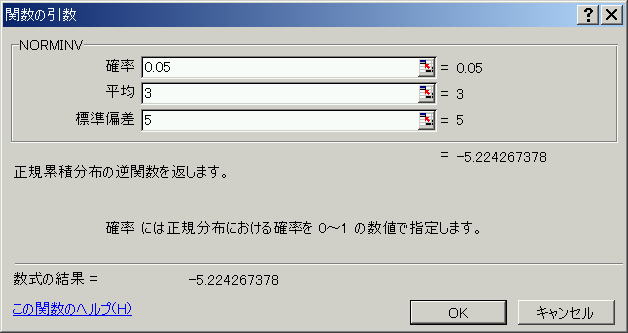
![]() 注意点
注意点
NORMDIST(x,平均,標準偏差,関数形式)
x 関数に代入する値を指定します。
平均 対象となる分布の算術平均 (相加平均) を指定します。
標準偏差 対象となる分布の標準偏差を指定します。
関数形式 計算に使用する指数関数の形式を論理値で指定します。関数形式に
TRUE を指定すると累積分布関数の値が計算され、FALSE を指定すると確率密度関数の値が計算されます。
NORMINV(確率,平均,標準偏差)
確率 正規分布における確率を指定します。
平均 対象となる分布の算術平均 (相加平均) を指定します。
標準偏差 対象となる分布の標準偏差を指定します。
NORMSDIST(z)
z 関数に代入する値を指定します。
NORMSDIST(z)
z 関数に代入する値を指定します。
TDIST(x,自由度,尾部)
x t 分布を計算する数値を指定します。
自由度 分布の自由度を整数で指定します。
尾部 片側分布を計算するか両側分布を計算するか、数値で指定します。尾部に
1 を指定すると片側分布の値が計算され、2 を指定すると両側分布の値が計算されます。
TINV(確率,自由度)
確率 スチューデントの両側 t 分布に従う確率を指定します。
自由度 分布の自由度を指定します。
片側 t 値は、確率に 2*
確率を指定して返すこともできます。確率が 0.05、自由度が 10
の場合、両側値は TINV(0.05,10) で計算され、2.28139
が返されます。同じ確率と自由度に対する片側値は TINV(2*0.05,10)
で計算でき、1.812462 が返されます。
![]()
表1は家計調査における平成15年平均の勤労者世帯における都市階級・地方・都道府県庁所在市別1世帯当たり1か月間の収入と支出のうち、経常収入について東北地方と関東地方についてまとめたものである。東北地方と関東地方では経常収入に差があるかを検定したい。
① 分析ツールを用いて等分散性の検定を行いなさい。
② 分析ツールを用いて等分散を仮定した平均値の検定を行いなさい。
③ 分析ツールを用いて等分散を仮定しない平均値の検定を行いなさい。
④ エクセル統計を用いて分散未知の平均値の検定を行いなさい。
⑤ 結果についてまとめなさい。
![]()
例題では東北地方と関東地方を比較したいと思っています。この場合、東北地方と関東地方では対応はありませんから対応のないt検定を行う必要があります。対応のないt検定では分散が等しいかどうかにより方法が変わってきます。そこで等分散性の検定を行ったうえでその結果により使い分ける必要があります。今回は練習のため両方の検定を行って見ましょう。
![]()
![]()
ここでは分析ツールを用いた検定の方法をいくつか紹介します。
![]() ①
①![]()
まずは等分散の検定を行ってみましょう。
![]() 「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
![]() 「分析ツール」の中から「」を選び、「OK」を押します。
「分析ツール」の中から「」を選び、「OK」を押します。
![]() すると以下のダイアログボックスが出力されます。
すると以下のダイアログボックスが出力されます。
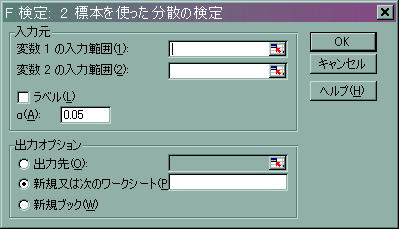
![]() 「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
![]() 「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
![]() 「ラベル」にチェックを入れてください。
「ラベル」にチェックを入れてください。
![]() 「出力オプション」では出力先を同じワークシートのデータの下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「A11」と指定してください。
「出力オプション」では出力先を同じワークシートのデータの下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「A11」と指定してください。
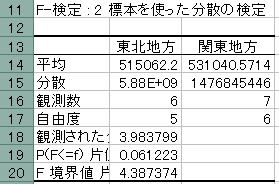
![]() 以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
![]()
![]()
ここでは等分散が仮定された場合の平均の検定について紹介します。
![]() 「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
![]() 「分析ツール」の中から「」を選び、「OK」を押します。
「分析ツール」の中から「」を選び、「OK」を押します。
![]() すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
![]() 「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
![]() 「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
![]() 仮説平均の差異には「0」と入力してください。
仮説平均の差異には「0」と入力してください。
![]() 「ラベル」にチェックを入れてください。
「ラベル」にチェックを入れてください。
![]() 「出力オプション」では出力先を同じワークシート等分散の結果の下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「A22」と指定してください。
「出力オプション」では出力先を同じワークシート等分散の結果の下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「A22」と指定してください。
![]() 以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
![]()
![]()
ここでは等分散が仮定されない場合の平均の検定について紹介します。
![]() 「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
![]() 「分析ツール」の中から「」を選び、「OK」を押します。
「分析ツール」の中から「」を選び、「OK」を押します。
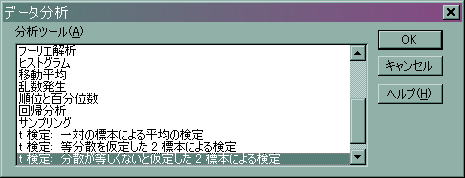
![]() すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
![]() 「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
「変数1の入力範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
![]() 「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
「変数2の入力範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
![]() 仮説平均の差異には「0」と入力してください。
仮説平均の差異には「0」と入力してください。
![]() 「ラベル」にチェックを入れてください。
「ラベル」にチェックを入れてください。
![]() 「出力オプション」では出力先を同じワークシート等分散の結果の右に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「E22」と指定してください。
「出力オプション」では出力先を同じワークシート等分散の結果の右に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「E22」と指定してください。
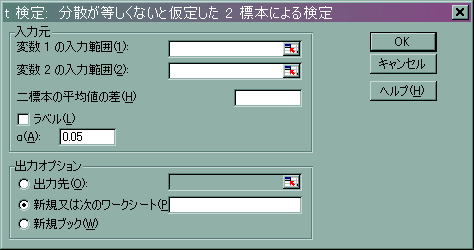
![]() 以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
![]()
![]()
エクセル統計2002を用いると上記の3つの結果が一括で出力されます。エクセル統計で分析を行って見ましょう。
![]() 「エクセル統計」⇒「平均の推定・検定」⇒「対応のない2群の差の検定」として左クリックを押します。
「エクセル統計」⇒「平均の推定・検定」⇒「対応のない2群の差の検定」として左クリックを押します。
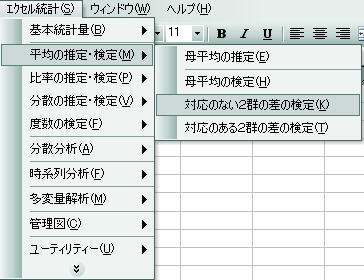
![]() すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
![]() 「変数(1)の範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
「変数(1)の範囲」には東北地方のデータを範囲として指定します。(東北地方というタイトルの行もラベルとして使用したいので、「B2からB8」までを指定してください。
![]() 「変数(2)の範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
「変数(2)の範囲」には関東地方のデータを範囲として指定します。(関東地方というタイトルの行もラベルとして使用したいので、「C2からC9」までを指定してください。
![]() 「公式」では「t検定」にチェックを入れます。
「公式」では「t検定」にチェックを入れます。
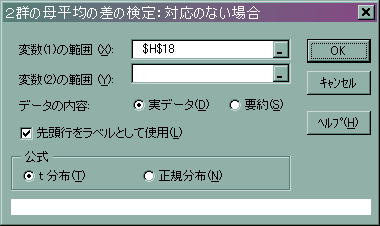
![]() 以上の作業ができたら「OK」を押してください。すると新しいワークシートに以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると新しいワークシートに以下のように結果が表示されます。
(本来ならば横に出力されていると思います)
![]()
![]()
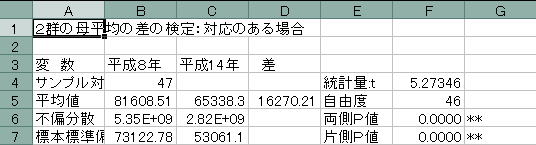
以上の作業で結果を出力することができました。これらから結果がどのようなことを表しているかを判断しなければなりません。特に検定では帰無仮説が「棄却される」のか「棄却されない」のかを判断する必要があります。結果を見ながら判断していきましょう。
![]() まず仮説検定では有意水準を設定しておくことが必要です。有意水準は「0.10」、「0.05」、「0.01」という値がよく用いられます。また仮説によって「両側検定」、片側検定」と使い分けることが必要です。この点は講義で説明しましたのでここでは有意水準5%(0.05)で両側検定をしているという元での解説を行います。
まず仮説検定では有意水準を設定しておくことが必要です。有意水準は「0.10」、「0.05」、「0.01」という値がよく用いられます。また仮説によって「両側検定」、片側検定」と使い分けることが必要です。この点は講義で説明しましたのでここでは有意水準5%(0.05)で両側検定をしているという元での解説を行います。
![]() 判断の仕方は次の方法があります。
判断の仕方は次の方法があります。
| P値から判断する場合 | 境界値から判断する場合 | |
| 棄却される場合 | P値が有意水準より小さい | |統計量|<境界値 |
| 棄却されない場合 | P値が有意水準より大きい | |統計量|>境界値 |
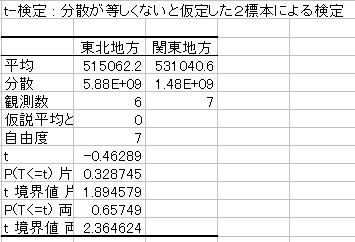
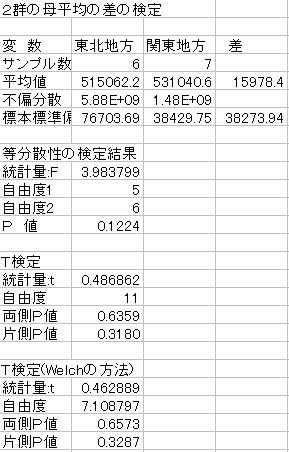
![]() 最初に「F検定」の結果を見てみましょう。これは等分散が仮定できるかを検定していました。
最初に「F検定」の結果を見てみましょう。これは等分散が仮定できるかを検定していました。

![]() 19行目の出力結果を見ます。P片側の確率は「B19」に出力されている0.061です。通常等分散の検定は両側検定を行うのでこの確率を2倍した値0.122446が両側確率になります。この値は0.05より大きくなっています。
19行目の出力結果を見ます。P片側の確率は「B19」に出力されている0.061です。通常等分散の検定は両側検定を行うのでこの確率を2倍した値0.122446が両側確率になります。この値は0.05より大きくなっています。
P値(0.122)>有意水準(0.05)より帰無仮説は棄却されない
ということになります。帰無仮説は「分散が等しい」という仮説でこれが棄却されないのですから等分散は仮定できるということになります。よってt検定は等分散を仮定した方法を用いていきます。
![]() F検定の結果によってt検定の方法が異なります。
F検定の結果によってt検定の方法が異なります。
F検定で棄却されない⇒等分散が仮定できる⇒「等分散を仮定したt検定」
F検定で棄却される⇒等分散が仮定できない⇒「等分散を仮定しないt検定」
今回は例題なのでt検定を2つ行いましたが、F検定の結果によって一方は使う必要がありません。今回は等分散を仮定したt検定を用いればよいので等分散が仮定できないほう方の結果は用いません。
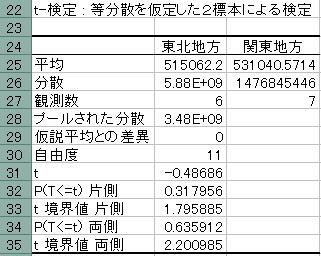
![]() 等分散を仮定した場合の結果についてみてみます。
等分散を仮定した場合の結果についてみてみます。

両側検定を行っているので見るべきところは34行目のP値両側の確率です。P両側の確率は「B34」に出力されている0.635912です。この値は0.05より大きくなっています。
P値(0.636)>有意水準(0.05)より帰無仮説は棄却されない
ということになります。帰無仮説は「平均が等しい」という仮説でこれが棄却されないのですから平均は等しくないとはいえないということになります。
![]() エクセル統計の結果も同様に見ていきます。なお、帰無仮説が棄却される場合は「有意」と出力されます。この場合は「有意」な(意味のある)差があると判断していきます。
エクセル統計の結果も同様に見ていきます。なお、帰無仮説が棄却される場合は「有意」と出力されます。この場合は「有意」な(意味のある)差があると判断していきます。
平均の検定の場合は有意な差があることを「有意差あり」といいます。また棄却されない場合には「有意差なし」といいます。
![]()
![]()
ここでは結果の記述の仕方について解説します。
![]() 結果の記述は以下の点に注意して書いていきます。
結果の記述は以下の点に注意して書いていきます。
![]() 比較する2つの標本
比較する2つの標本
![]() 等分散性の検定の結果
等分散性の検定の結果
![]() 母平均の差の検定と用いる公式と結果
母平均の差の検定と用いる公式と結果
記述例は講義資料を参考にしてください。
![]()
表2は平成8年と平成14年における住宅地平均価格(円/㎡)の都道府県別データである。この間に土地価格に有意な差があったか検定したい。
① 分析ツールを用いて等分散を仮定した平均値の検定を行いなさい。
② 分析ツールを用いて1対の標本による平均値の検定を行いなさい。
③ ①と②の結果に違いがあることを確認しなさい。
④ エクセル統計を用いて対応のある平均値の検定を行いなさい。
⑤ 結果についてまとめなさい。
![]()
例題では平成8年と平成14年を比較したいと思っています。この場合、どの都道府県も8年と14年のデータがありますから都道府県ごとに対応のあるデータになっています。よって対応のあるt検定を行う必要があります。ここでは対応のあるデータに対する平均値の検定を行いましょう。
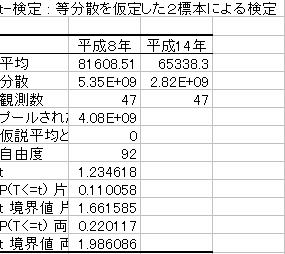
![]() ① 等分散を仮定した平均値の検定は例題1で行いました。同様の方法で行いましょう。
① 等分散を仮定した平均値の検定は例題1で行いました。同様の方法で行いましょう。
![]() 結果は「E1」に出力させましょう。
結果は「E1」に出力させましょう。
![]() ②
②![]()
ここでは対応のある場合の平均の検定について紹介します。
![]() 「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
「ツール」⇒「分析ツール」として左クリックを押します。すると以下のダイアログボックスが出力されます。
![]() 「分析ツール」の中から「」を選び、「OK」を押します。
「分析ツール」の中から「」を選び、「OK」を押します。
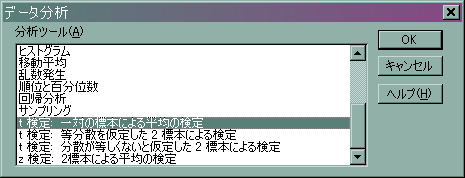
![]() すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
![]() 「変数1の入力範囲」には平成8年のデータを範囲として指定します。(平成8年というタイトルの行もラベルとして使用したいので、「B2からB49」までを指定してください。
「変数1の入力範囲」には平成8年のデータを範囲として指定します。(平成8年というタイトルの行もラベルとして使用したいので、「B2からB49」までを指定してください。
![]() 「変数2の入力範囲」には平成14年のデータを範囲として指定します。(平成14年というタイトルの行もラベルとして使用したいので、「C2からC49」までを指定してください。
「変数2の入力範囲」には平成14年のデータを範囲として指定します。(平成14年というタイトルの行もラベルとして使用したいので、「C2からC49」までを指定してください。
![]() 仮説平均の差異には「0」と入力してください。
仮説平均の差異には「0」と入力してください。
![]() 「ラベル」にチェックを入れてください。
「ラベル」にチェックを入れてください。
![]() 「出力オプション」では①の結果の下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「E17」と指定してください。
「出力オプション」では①の結果の下に出力させたいので「出力先」にチェックし、右の範囲を指定する部分に「E17」と指定してください。
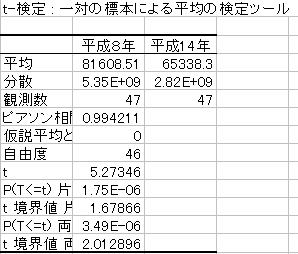
![]() 以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると以下のように結果が表示されます。
![]() ④
④![]()
エクセル統計で分析を行って見ましょう。
![]() 「エクセル統計」⇒「平均の推定・検定」⇒「対応のある2群の差の検定」として左クリックを押します。
「エクセル統計」⇒「平均の推定・検定」⇒「対応のある2群の差の検定」として左クリックを押します。
![]() すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
すると以下のダイアログボックスが出力されます。入力の仕方は先ほどとほぼ同じです。
![]() 「変数(1)の範囲」には平成8年のデータを範囲として指定します。(平成8年というタイトルの行もラベルとして使用したいので、「B2からB49」までを指定してください。
「変数(1)の範囲」には平成8年のデータを範囲として指定します。(平成8年というタイトルの行もラベルとして使用したいので、「B2からB49」までを指定してください。
![]() 「変数(2)の範囲」には平成14年のデータを範囲として指定します。(平成14年というタイトルの行もラベルとして使用したいので、「C2からC49」までを指定してください。
「変数(2)の範囲」には平成14年のデータを範囲として指定します。(平成14年というタイトルの行もラベルとして使用したいので、「C2からC49」までを指定してください。
![]() 「公式」では「t検定」にチェックを入れます。
「公式」では「t検定」にチェックを入れます。
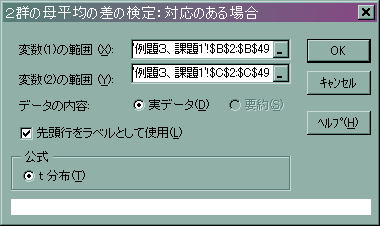
![]() 以上の作業ができたら「OK」を押してください。すると新しいワークシートに以下のように結果が表示されます。
以上の作業ができたら「OK」を押してください。すると新しいワークシートに以下のように結果が表示されます。
![]()
例題3において平成14年の住宅地平均価格(円/㎡)について東北地方と関東地方では差があるかを検定したい。
①
エクセル統計を用いて検定を行いなさい。
②
結果についてまとめなさい。
![]()
例題1のように東北地方と関東地方のデータをまとめなおすと同じ方法で行えます。
![]()
表3は家計調査における平成15年平均の勤労者世帯と全世帯における都市階級・地方・都道府県庁所在市別1世帯当たり1か月間の収入と支出のうち、消費支出についてまとめたものである。
(1)勤労者世帯と全世帯では消費支出に差があるかを検定したい。
①
エクセル統計を用いて検定を行いなさい。
②
結果についてまとめなさい。
![]()
例題2のように対応のあるt検定を行います。
![]()
課題1のように対応のないt検定を行います。