

第8回 重回帰分析
![]()
![]() これからエクセル統計を用いてたくさんの分析を行います。エクセル統計では新たなワークシートに結果が表示されます。よって、どのワークシートに結果が出力されているかを見つけるのが大変になってきます。エクセル統計で分析した後はワークシートに何の分析をしたのかがわかるように名前をつけていく習慣をつけていきましょう。ワークシートの名前の変更の仕方はワークシートの名前がある「Sheet?」となっている部分をダブルクリックします。色が反転したら名前を入力してください。入力後どこか適当なセルをクリックして名前が変更していれば変更できました。
これからエクセル統計を用いてたくさんの分析を行います。エクセル統計では新たなワークシートに結果が表示されます。よって、どのワークシートに結果が出力されているかを見つけるのが大変になってきます。エクセル統計で分析した後はワークシートに何の分析をしたのかがわかるように名前をつけていく習慣をつけていきましょう。ワークシートの名前の変更の仕方はワークシートの名前がある「Sheet?」となっている部分をダブルクリックします。色が反転したら名前を入力してください。入力後どこか適当なセルをクリックして名前が変更していれば変更できました。
![]() 解答欄には回帰式を答えてもらうケースがあります。この場合には分析結果のセルをコピーして解答欄のセルに貼り付けて答えてください。
解答欄には回帰式を答えてもらうケースがあります。この場合には分析結果のセルをコピーして解答欄のセルに貼り付けて答えてください。
⇒セルを選択してコピー
解答欄に貼り付ける
![]()
変数選択などにより選択されなかった部分は入力しない!
↓
![]()
![]()
表1は,失業者数(Y)と就業者数の合計と各産業の就業者数(第1次、第2次、第3次産業)の都道府県データをまとめたものです。
(1) 失業者数(Y)に対する就業者数(X)の回帰分析について分析ツールを用いておこない、回帰式と決定係数を答えなさい.
(2) 就業者数が1000人増加すると失業者はどのように変化すると思われますか?
(3) 失業者数(Y)に対する第1次(A)、第2次(B)、第3次産業就業者数(C)の重回帰分析について分析ツールを用いて結果を出力し、重回帰式と修正済決定係数を答えなさい.
(4) (3)の操作についてエクセル統計を用いて行い結果を出力し、重回帰式と修正済決定係数を答えなさい.なお、変数選択は全変数としておいて下さい.
(5) (3)の操作について再度エクセル統計を用いて行い結果を出力し、重回帰式と修正済決定係数を答えなさい.なお、変数選択は増減法としておいて下さい.
(6) (3)〜(5)の出力結果を比較して気づいたことをまとめなさい.
(7) (5)の操作について再度エクセル統計を用いて行い結果を出力し、重回帰式と修正済決定係数を答えなさい.なお、変数選択は増減法としてF値をそれぞれ3.0と設定しておいて下さい.
(8) (7)の結果から選択された変数を答えなさい。
(9) (8)の変数のうち、意味のある変数はどれですか?
(10) (6)の結果から第1次、第2次、第3次産業の中で最も失業者に影響を与えているのは何次産業ですか?またその理由を答えなさい.
(11) 都道府県の中で一番就業状態がよい都道府県と一番悪い都道府県はどこですか?
(12) 失業者に対する残差グラフを作成し,動向を考察しなさい.

単回帰分析は先週行いました。(2)までは自分で行いましょう。
前回の単回帰分析分析の場合、分析ツールやエクセル統計では目的変数や説明変数は1つの行だけを範囲として指定していました。しかし重回帰分析のように複数の説明変数を範囲として指定することもできます。
![]()
![]()
![]() 手順1 まずメニューから「ツール」⇒「分析ツール(D)」を選択し,データ分析画面を出力させます。
手順1 まずメニューから「ツール」⇒「分析ツール(D)」を選択し,データ分析画面を出力させます。
![]() 手順2 回帰分析を選択して「OK」を押します.
手順2 回帰分析を選択して「OK」を押します.
![]() 手順3 「Y入力範囲」には変数Yのデータ範囲を指定し、「X入力範囲」には変数Xのデータ範囲を指定します。今は
手順3 「Y入力範囲」には変数Yのデータ範囲を指定し、「X入力範囲」には変数Xのデータ範囲を指定します。今は
Y:失業者の入っているB2からB49までを指定します。
X:第1次産業から第3次産業まですべてのデータを指定しますからD2からF49までを指定します。
今回はすべてにチェックしておきましょう。最後に「OK」を押します.
 |
![]() 手順4 これで以下の出力結果が得られます。
手順4 これで以下の出力結果が得られます。
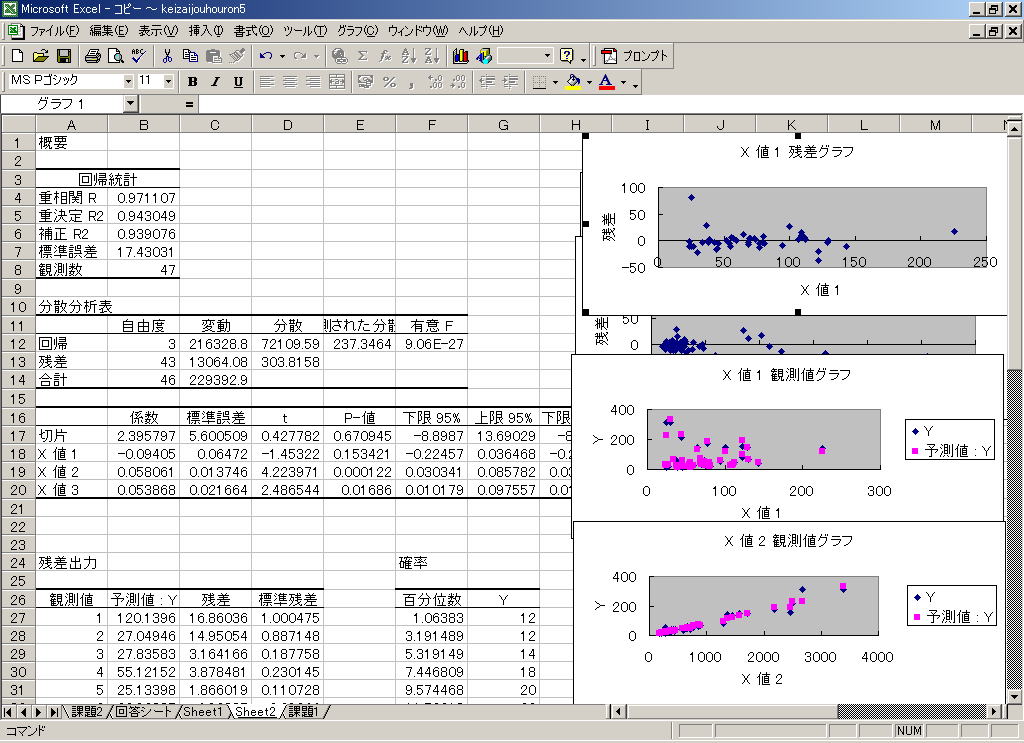 |
![]() 手順5 得られた結果の出力画面のうち以下の項目に注目します.
手順5 得られた結果の出力画面のうち以下の項目に注目します.
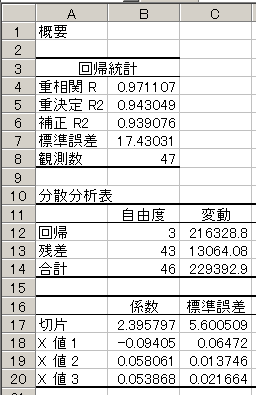
これから回帰式は
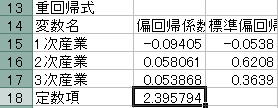
Y=2.395797-0.09405 A+0.058 B+0.053868 C
となり、決定係数は0.943049となります。ただし重回帰分析の場合には修正済決定係数を用いた方が当てはまりのよさがしっかりと判断できます。この値はここでは補正R2の0.939076という値です.
![]()
![]()
![]() 手順1 メニューから「エクセル統計」⇒多変量解析⇒「重回帰分析」を選択する。
手順1 メニューから「エクセル統計」⇒多変量解析⇒「重回帰分析」を選択する。
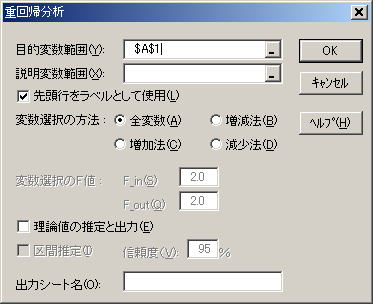
![]() 手順2 目的変数範囲にはYとする変数の範囲を指定する
手順2 目的変数範囲にはYとする変数の範囲を指定する
![]() 手順3 説明変数範囲にはXとする変数の範囲を指定する
手順3 説明変数範囲にはXとする変数の範囲を指定する
![]() 手順4 変数選択の方法は問題によってチェックを変える。
手順4 変数選択の方法は問題によってチェックを変える。
(何も指定がない場合には増減法がおすすめ)
![]() 手順5 変数選択のF値は今回はそのまま
手順5 変数選択のF値は今回はそのまま
![]() 手順6 理論値の推定と出力にチェックを入れる。
手順6 理論値の推定と出力にチェックを入れる。
![]() 手順7 OKを押す。
手順7 OKを押す。
 |
![]() 手順8 これにより以下の出力結果が得られます。
手順8 これにより以下の出力結果が得られます。
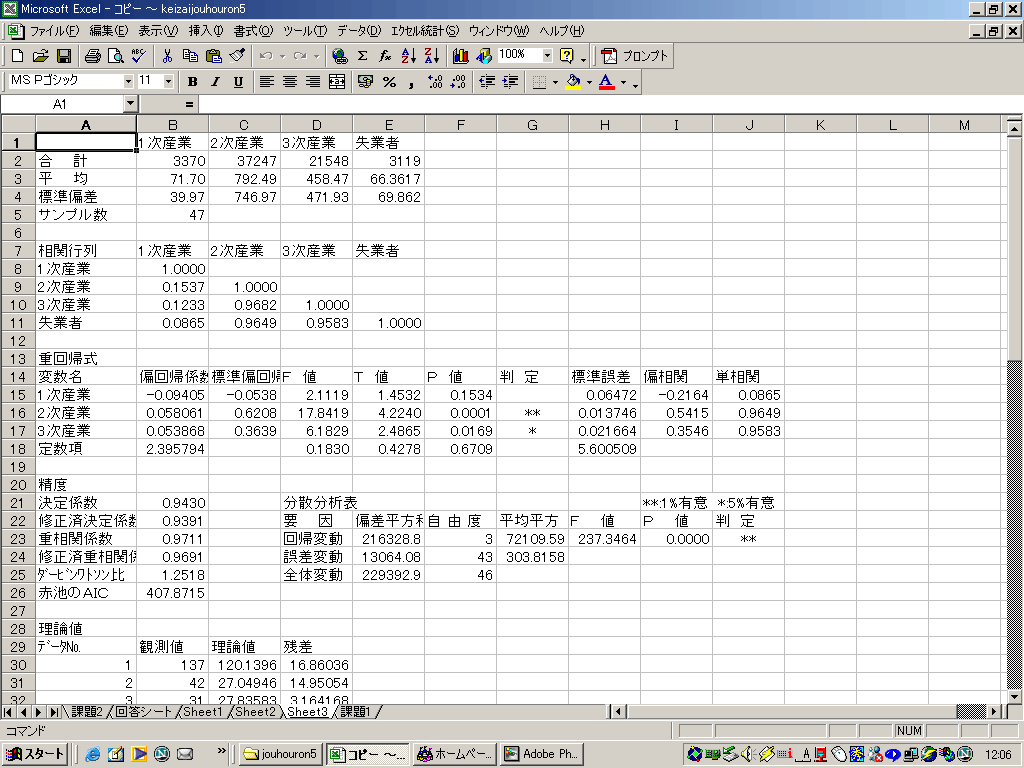
![]() 手順9 得られた結果の出力画面のうち以下の項目に注目します.
手順9 得られた結果の出力画面のうち以下の項目に注目します.
![]() 1行目から5行目までは各変数の基本統計量が出力されています.この結果からデータの位置やデータの散らばりを考えていきます.
1行目から5行目までは各変数の基本統計量が出力されています.この結果からデータの位置やデータの散らばりを考えていきます.
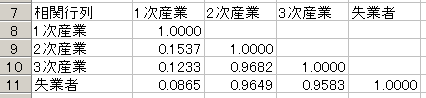
![]() 7行目からは相関行列が出力されています.これから変数間の関係を考えていきます.
7行目からは相関行列が出力されています.これから変数間の関係を考えていきます.
また多重共線性の吟味などを行います.
多重共線性の吟味を行う場合には説明変数間の相関係数をみます。(ここでは失業者は関係ない!!)
2次産業と3次産業の相関係数が0.9682と高いので多重共線性を起こしている可能性は十分あります.
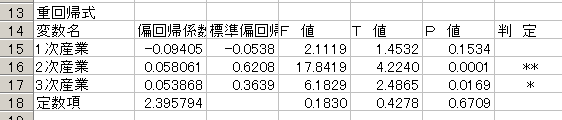
![]() 13行目からは重回帰分析結果が出力されています.
13行目からは重回帰分析結果が出力されています.
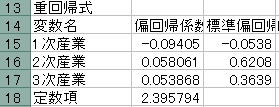
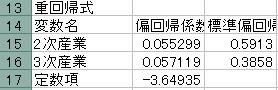
![]() B列の偏回帰係数から重回帰式を求めます。ここでは
B列の偏回帰係数から重回帰式を求めます。ここでは
Y=−0.09405A+0.058061B+0.053868C+2.395794
となりました。
![]() C列の標準偏回帰係数は偏回帰係数の値を基準化したものです。
C列の標準偏回帰係数は偏回帰係数の値を基準化したものです。
説明変数の重要度を表わしています。
プラスマイナスに関係なく数字が大きい順に重要度を表わしています。
ここでは2次産業⇒3次産業⇒1次産業の順になっています。
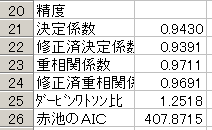
![]() 20行目からは重回帰分析の精度を出力しています。
20行目からは重回帰分析の精度を出力しています。
この中で特に重要なのは修正済決定係数です.
この授業では当てはまりのよさについて次の基準で考えましょう.
| 決定係数の値 | 判断 |
| 0.9以上 | 非常に当てはまりがよい |
| 0.7以上0.9未満 | 当てはまりがよい |
| 0.5以上0.7未満 | あまり当てはまりはよくない |
| 0.5未満 | 当てはまりは悪い |
ここでは0.9391となりましたから非常に当てはまりがよいと判断します。
![]() 28行目からは観測値と理論値の値が表示されます.
28行目からは観測値と理論値の値が表示されます.
データNoは各データ番号で今は都道府県データになります。よって
都道府県名を貼り付けておきましょう。
![]() このデータを用いて残差分析を行います.
このデータを用いて残差分析を行います.
残差が最も大きいのは大阪府
最も小さいのは愛知県とわかりました。
![]()
![]() 重回帰分析を行ううえで問題となるのは多重共線性を起こしているかが問題になります。簡単なチェック方法としては偏回帰係数の符号と単相関の符号が一致しているかが問題になります。全変数で行った場合、結果として
重回帰分析を行ううえで問題となるのは多重共線性を起こしているかが問題になります。簡単なチェック方法としては偏回帰係数の符号と単相関の符号が一致しているかが問題になります。全変数で行った場合、結果として

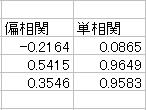
となった場合、1次産業の符号が異なります。よって多重l共線性を起こしていると判断されます。
また変数選択を行った(5)の結果もすべての産業が出力されていることから説明変数を減らすことができなかったという結果になります。
![]() 結果はすべて同じになった。また1次産業の偏回帰係数と単相関の符号が異なるため、多重l共線性を起こしていると考えられる。
結果はすべて同じになった。また1次産業の偏回帰係数と単相関の符号が異なるため、多重l共線性を起こしていると考えられる。
![]() 基本的には(5)の操作と同様の操作を行いますが、変数選択のF値の値をそれぞれ「3.0」と入力します。
基本的には(5)の操作と同様の操作を行いますが、変数選択のF値の値をそれぞれ「3.0」と入力します。
F値を高くすれば選択される条件が厳しくなり、変数が減る可能性があります。結果として以下の値が出力されたので1次産業は選択されなかったことになります。

![]() 変数名に出力されている変数が選択された変数です。 (7)の結果から選択された変数を答えなさい。
変数名に出力されている変数が選択された変数です。 (7)の結果から選択された変数を答えなさい。
![]() 2次産業、3次産業
2次産業、3次産業
![]() T値、P値、判定は回帰係数が0であるかの検定、つまり
T値、P値、判定は回帰係数が0であるかの検定、つまり
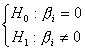
の結果を表しています。もし回帰係数が0であるならば説明変数の値が変化しても目的変数は変化しません。よってこのような場合にはその説明変数はあまり意味がありません。よって意味のある変数は仮説検定で棄却された変数を答えます。棄却されているかを判断するのは判定に「*」または「**」となっている変数が棄却されている変数です。この変数を答えましょう。
![]() 2次産業、3次産業
2次産業、3次産業
![]() (6)の結果から第1次、第2次、第3次産業の中で最も失業者に影響を与えているのは何次産業ですか?またその理由を答えなさい.
(6)の結果から第1次、第2次、第3次産業の中で最も失業者に影響を与えているのは何次産業ですか?またその理由を答えなさい.
(11) 都道府県の中で一番就業状態がよい都道府県と一番悪い都道府県はどこですか?
(12)
失業者に対する残差グラフを作成し,動向を考察しなさい.
説明力の大きさを表しているのは標準偏回帰係数でした。よって上の出力結果から2次産業が最も影響を与えていることがわかります。
![]() 2次産業
2次産業
![]() もし残差が大きければ理論的な値よりも観測値が高いということです。理論値は就業状態により予測される値ですから、理論値よりも観測値が高い県は予測される失業者よりも多いといえます。つまり残差が高い県は就業状態が悪いと判断できます。同様に都道府県の中で残差が低い県は就業状態がよいと判断できます。残差が最も高い県は大阪府で一番低いのは愛知県でしたからこれらが就業状態の最もよい県と悪い県になります。
もし残差が大きければ理論的な値よりも観測値が高いということです。理論値は就業状態により予測される値ですから、理論値よりも観測値が高い県は予測される失業者よりも多いといえます。つまり残差が高い県は就業状態が悪いと判断できます。同様に都道府県の中で残差が低い県は就業状態がよいと判断できます。残差が最も高い県は大阪府で一番低いのは愛知県でしたからこれらが就業状態の最もよい県と悪い県になります。
![]()
よい県 愛知県
悪い県 大阪府

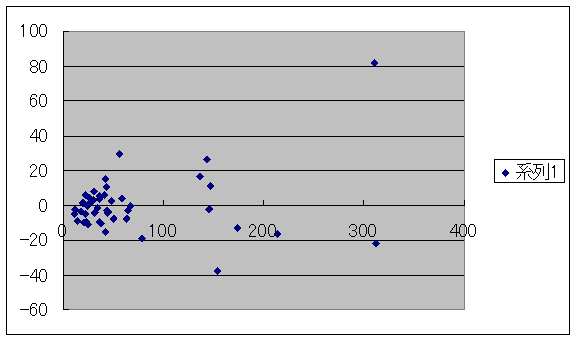
図からわかるように、失業者が増えれば残差も増えているという傾向が見られます。この結果は当然の結果ともいえますね。
![]()
![]()
(2)までは自分で行いましょう。
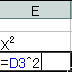
![]() 労働者の年齢であるXとその2乗したX2の2つの変数が説明変数である重回帰分析として考えます。説明変数の範囲を指定する場合、列が隣り合っていたほうがよいのでD列、E列に以下の関数を入力していきます。最初の階級「〜17歳」がある3行目にいかの関数を入力し、関数をその他のセルに貼り付けます。
労働者の年齢であるXとその2乗したX2の2つの変数が説明変数である重回帰分析として考えます。説明変数の範囲を指定する場合、列が隣り合っていたほうがよいのでD列、E列に以下の関数を入力していきます。最初の階級「〜17歳」がある3行目にいかの関数を入力し、関数をその他のセルに貼り付けます。
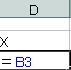
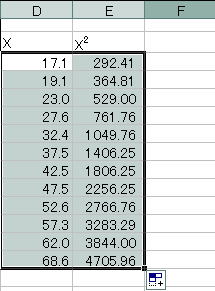
この結果から目的変数をC列、説明変数をD,E列として重回帰分析を行います。なお、変数選択はしたくないので「全変数」で分析します。
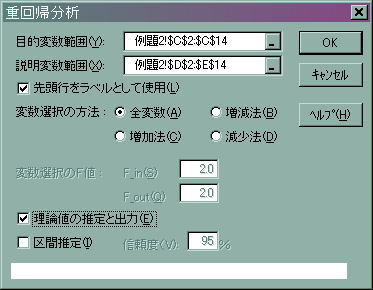
この結果、以下の出力結果が得られました。
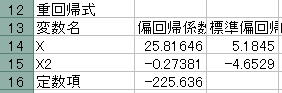

よって重回帰式は
Y=-225.636+25.81646X-0.27381X2
となり、修正済決定係数は0.9519と得られました。
![]() (1)で作成した散布図に(2)、(3)の結果を追加します。
(1)で作成した散布図に(2)、(3)の結果を追加します。
(2)の散布図は例題2のB列と回帰分析出力結果の理論値、
(3)の散布図は例題2のB列と重回帰分析出力結果の理論値で追加していきます。
![]() モデルのよさは当てはまりのよさで判断します。この場合には修正済決定係数が高い方を答えていきます。
モデルのよさは当てはまりのよさで判断します。この場合には修正済決定係数が高い方を答えていきます。
表4は,家計調査における経常収入(Y)と消費支出を10分類したときの各消費支出の都道府県データをまとめたものです。
( 1)経常収入(Y)に対する10分類したときの各消費支出を説明変数として重回帰分析を行いなさい.なお,変数選択では増減法を用いなさい.
(2) 経常収入と最も関係のある項目はどれですか?
(3) 全変数で重回帰分析を行う場合,多重共線性を起こしていると思われますか?またその理由について書きなさい.
(4) 変数選択で選ばれた項目を挙げなさい.
(5) 選ばれた項目の中で意味のある変数はどれですか?
(6) 選ばれた項目の中でどの項目が経常収入に最も影響していると思われますか?
(7) 経常収入に対する残差グラフを作成し,動向を考察しなさい.
(8) 都道府県の中で一番貯蓄率がよいのはどこの都道府県ですか
![]()
表5は2005年におけるわが国の大卒男女別現金給与額(月間、千円)Yと労働者の年齢Xの関係を示しています。あなたの性別のデータを用いて以下の課題を行いなさい。
(1)横軸にX,縦軸にYをとり、散布図を描きなさい。
(2)重回帰モデル
![]()
をOLSで推定し、自由度修正済決定係数を求めなさい。
(3)(2)の回帰式を(1)の散布図に加えなさい。