![]()
![]()
|
|
![]() 手順1 メニューから「エクセル統計」⇒多変量解析⇒「主成分分析」を選択する。
手順1 メニューから「エクセル統計」⇒多変量解析⇒「主成分分析」を選択する。
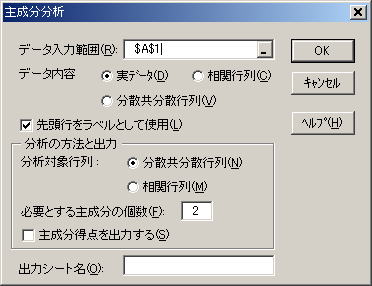
![]() 手順2 データ入力範囲にはすべての変数のデータの範囲を指定する
手順2 データ入力範囲にはすべての変数のデータの範囲を指定する
![]() 手順3 分析対象行列は相関行列にチェックする
手順3 分析対象行列は相関行列にチェックする
![]() 手順4 「主成分得点を出力する」のチェックボックスにチェックを入れる
手順4 「主成分得点を出力する」のチェックボックスにチェックを入れる
![]() 手順5 OKを押す。
手順5 OKを押す。
![]() 手順6 これにより以下の出力結果が得られます。
手順6 これにより以下の出力結果が得られます。
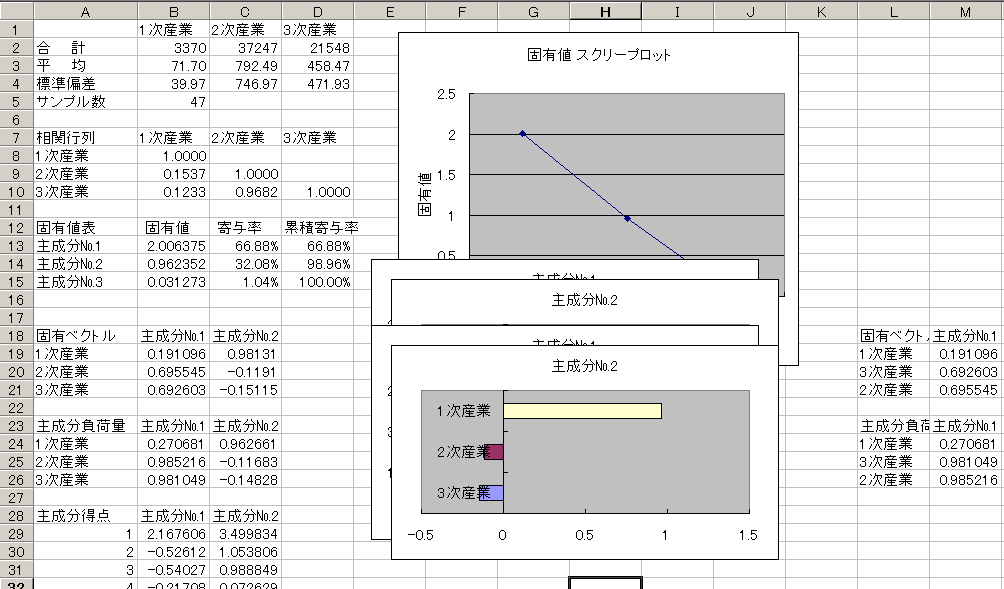
![]() 手順7 得られた結果の出力画面のうち以下の項目に注目します.
手順7 得られた結果の出力画面のうち以下の項目に注目します.
![]() 1行目から5行目までは各変数の基本統計量が出力されています.この結果からデータの位置やデータの散らばりを考えていきます.
1行目から5行目までは各変数の基本統計量が出力されています.この結果からデータの位置やデータの散らばりを考えていきます.

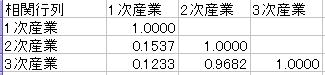
![]() 7行目からは相関行列が出力されています.これから変数間の関係を考えていきます.
7行目からは相関行列が出力されています.これから変数間の関係を考えていきます.
![]() 12行目からは固有値表の結果が出力されています.
12行目からは固有値表の結果が出力されています.
この中で特に寄与率、累積寄与率をチェックします.
寄与率は情報の集約の大きさで、この値が大きいほど集約力が高いといえます.
13行目の主成分No.1は66.88%の情報を持っていることがわかります.
また、累積寄与率は寄与率の合計が出力されています.この結果から主成分No.2までで98.65%の情報を保持していることがわかります.

![]() 18行目からは固有ベクトルの値が出力されています.
18行目からは固有ベクトルの値が出力されています.

固有ベクトルから各主成分が数式によって表されます.
よって第1主成分は
第2主成分は
と表されます.
![]() 23行目からは主成分負荷量の値が出力されています.
23行目からは主成分負荷量の値が出力されています.
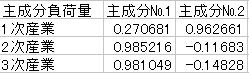
主成分負荷量の値から主成分の意味付けを行っていきます.
主成分負荷量は元の変数(データ)と新たに生成した変数(主成分)との相関係数を計算しています.
よって主成分負荷量が1や−1に近ければ関係が高いということです.
![]() 第1主成分は2次産業、と3次産業の主成分負荷量が高くなっています.
第1主成分は2次産業、と3次産業の主成分負荷量が高くなっています.
よって第1主成分は1次産業以外の就業者数と意味付けられます.
![]() 第2主成分は1次産業の主成分負荷量が高くなっています.
第2主成分は1次産業の主成分負荷量が高くなっています.
よって第2主成分は1次産業の就業者数と意味付けられます.
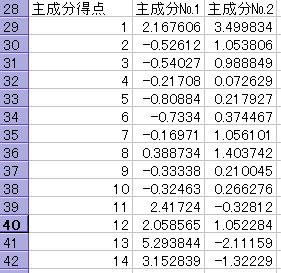
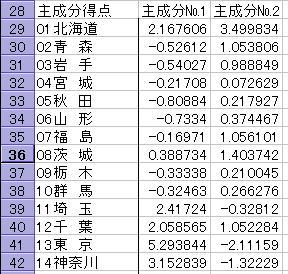
![]() 28行目からは主成分得点の値が出力されています.
28行目からは主成分得点の値が出力されています.
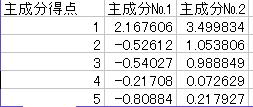
この得点の値からもとのデータの特徴がわかります.
なおA列にある数値はデータ番号でここでは北海道、青森の順になっています.
作業1 主成分負荷量のグラフを整形する!
エクセル統計では主成分分析を行う場合グラフも同時に出力されます.グラフは
(固有ベクトルと主成分負荷量の2種類)×(主成分の数)
の個数分出力されます.このグラフのなかで主成分負荷量のグラフを見やすい形に直してみます.
主成分の意味付けを行う上でグラフを見ながら行うとわかりやすくなるでしょう.
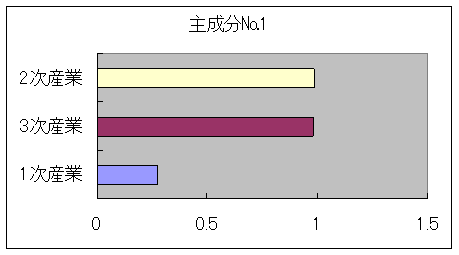
![]() 数値軸の設定
数値軸の設定
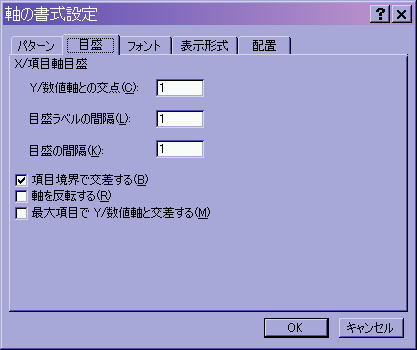
横軸が−1から1まで表示されるように数値軸の「軸の書式設定」⇒「目盛」で以下の図のようにする.
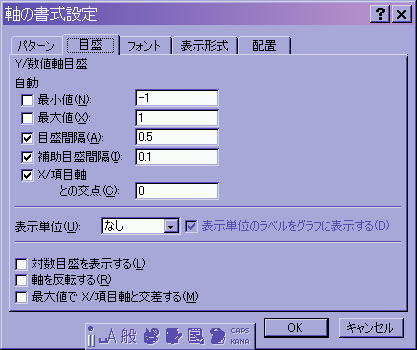
![]() 項目軸の設定
項目軸の設定
縦軸の項目がすべて表示されるようにします.(例題では関係ありません)
「軸の書式設定」⇒「目盛」で目盛ラベルの間隔を1とするとすべての項目が表示されます.
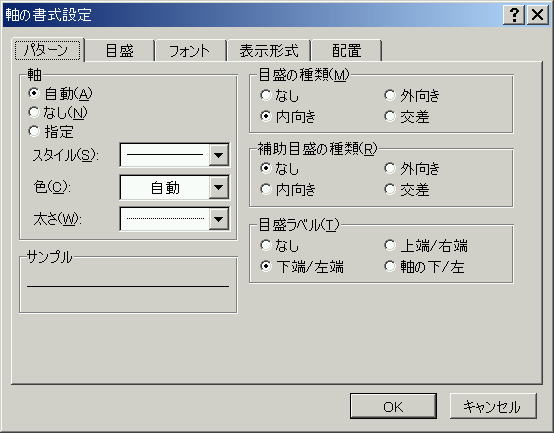
「軸の書式設定」⇒「パターン」でメモリラベルを下端/左端を選択する
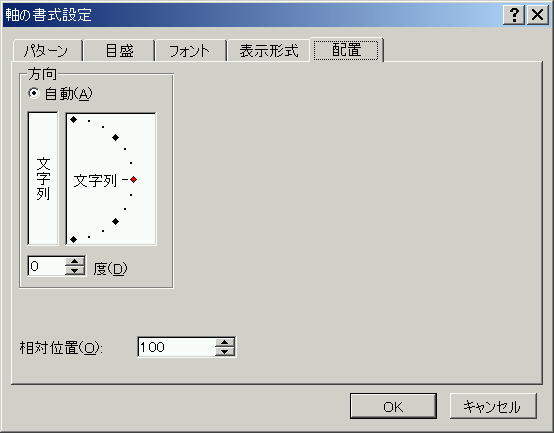
「軸の書式設定」⇒「配置」で0度に出力されるようにする
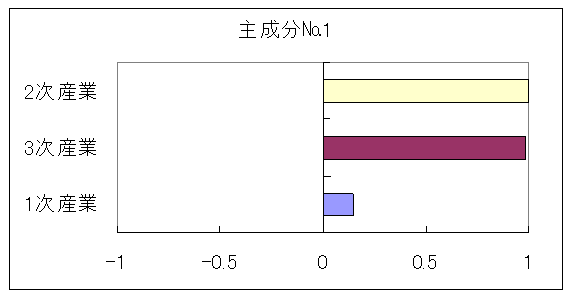
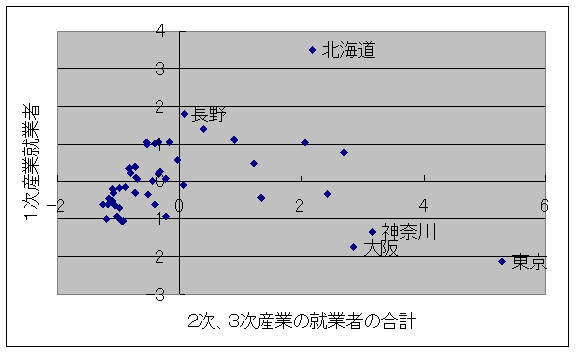
これにより以下のグラフに整形できました.主成分No2も同様に行ってみてください.
 |
⇒ |  |

論文に回帰分析の結果を記述する際には最低、以下のような内容を盛り込むこと
1.主成分分析を行う変数
2.寄与率と情報の大きさ
3.主成分負荷量と変数のネーミング
4.主成分得点の散布図からデータの特徴