第３回　経済分析のための数学、統計学の基礎

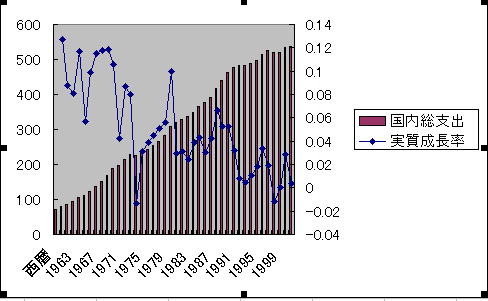
表１は、わが国の実質国内総生産（実質GDP）の推移を示したものです。
�@       実質国内総生産の推移の棒グラフを作成しなさい。
�A       実質成長率を計算しなさい。
�B       �@のグラフに実質成長率の折れ線グラフを作成しなさい。なお目盛りは第二軸に設定すること
�C       「神武景気」、「岩戸景気」を含む、１９５５年から６１年までの実質経済成長率（実質GDP成長率）を求めなさい。

�@棒グラフの作成は以下を参考にしてください。

�A実質成長率とはGDPなど成長が見込まれる指標の変化率を表しています。変化率は以下の公式で計算できます。



まずは「C3」に以下の式を入力します。

＝B3/B2-1



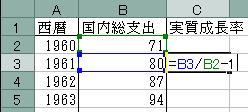
「C3]に結果が出力されたらセルの右下にマウスを移動しマウスの矢印が＋に変わったら左クリックを押しながら最後の「C43」まで移動し、左クリックを離します。



�@で作成したグラフに実質成長率を加えます。
下の図のようにグラフエリア（グラフの白の部分）にマウスを持っていき、グラフエリアと表示されたら右クリックを押し、メニューを表示させます。



メニューから「元のグラフ」を選択し、左クリックを押します。


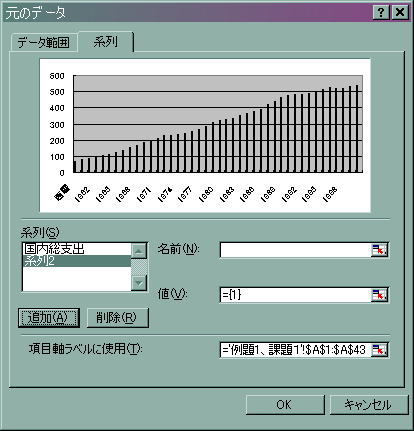
系列の追加ボタンを押します。
「値（V)」の欄に計算した成長率の値を指定します。
注意；変化率は２番目のデータからしか計算できません。現在の例では「C2」は空白になっています。しかし同じ項目軸を使う都合上、成長率は空白であるC2から指定してください。

「名前（N）」の欄には「実質成長率」と入力します。

「OK」を押します。

再度グラフエリア（グラフの白の部分）にマウスを持っていき、グラフエリアと表示されたら右クリックを押し、メニューを表示させます。

メニューから「グラフの種類」を選択し、左クリックを押します。




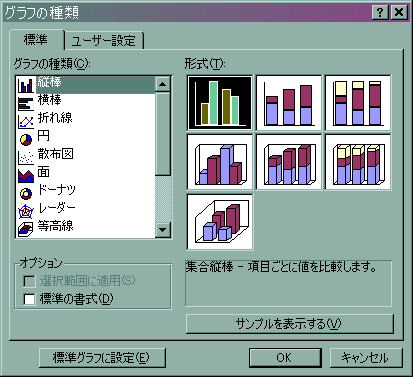
「ユーザー設定」を押し、２軸上の折れ線と縦棒を選択し「OK」を押します。

これでできあがり。




�C複数年の変化率を計算する場合は幾何平均を計算します。幾何平均とは
幾何平均＝
で計算されます。ここではｎ乗根を表しています。エクセルで計算する場合は

=(?????)^(1/n)
と1/n乗してあげればいいのです。

１９６５年から７０年までの６年間の平均ですから１９６５年から７０年までの成長率に1を加えたものを掛けて６乗根を計算すれば６５年から７０年までの幾何平均が計算できます。まずD列に１を加える計算をします。たとえば「D7」に

＝C7+1

と入力します。計算したい「F2」に以下の式を入力します。

＝（D7*D8*D９*D１０*D11*D１２）＾（１/６）−１



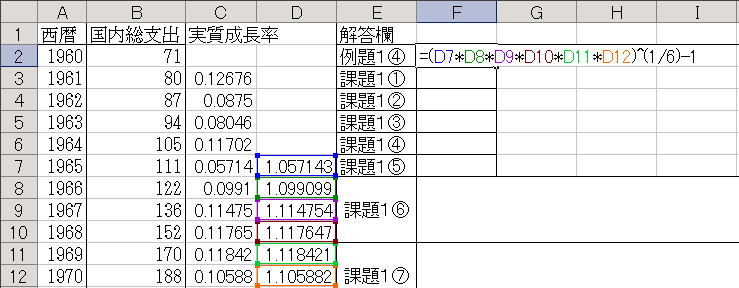
これから０．１０１４９という値が得られました。％に直すと10.149％です。この時期は約１０％の成長率があったことがわかります。

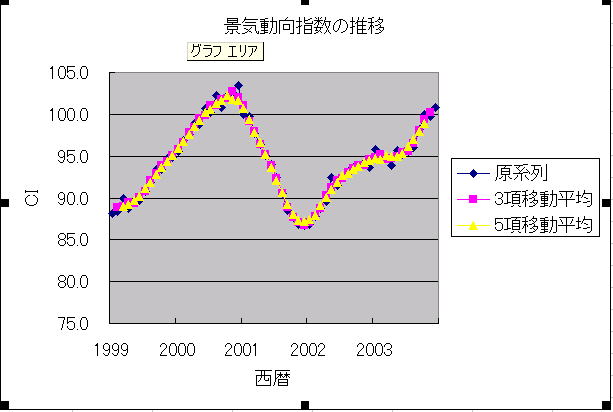
例題２（３項移動平均）表２は景気動向指数（CI）の一致系列について１９９９年１月から２００３年１２月までの数値である

�@        景気動向指数（CI）の一致系列の原系列について折れ線グラフを作成しなさい。

�A        ３項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。

�B        ５項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。

�@折れ線グラフの作成は以下を参考にしてください。

�A、�B移動平均は以下の公式で計算できます。項数が増えるごとに計算できない部分が多くなってきます。

	公式	計算できないところ
３項移動平均		最初と最後１つずつ計２個
５項移動平均		最初と最後２つずつ計４個
７項移動平均		最初と最後３つずつ計６個

３項移動平均を計算してみましょう。
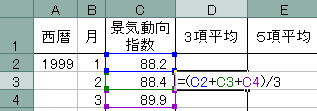
D列最初の「D2」は計算できないので「D3」から計算します。
計算したい「D3」に以下の式を入力します。

＝（C2+C3+C4）/３

「D3]に結果が出力されたらセルの右下にマウスを移動しマウスの矢印が＋に変わったら左クリックを押しながら最後の1個前である「D６０」まで移動し、左クリックを離します。

５項移動平均を計算してみましょう。
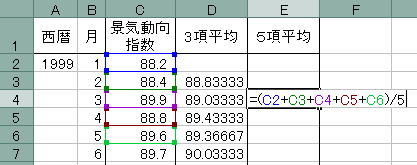
E列最初の２つ「E2」、「E3」は計算できないので「E4」から計算します。
計算したい「E4」に以下の式を入力します。

＝（C2+C3+C4＋C5+C6）/５

「E4」に結果が出力されたらセルの右下にマウスを移動しマウスの矢印が＋に変わったら左クリックを押しながら最後の２個前である「E59」まで移動し、左クリックを離します。

最後にグラフを原系列に追加します。

例題1と同じ方法でグラフを追加していきます。

下の図のようにグラフエリア（グラフの白の部分）にマウスを持っていき、グラフエリアと表示されたら右クリックを押し、メニューを表示させます。


メニューから「元のグラフ」を選択し、左クリックを押します。


系列の追加ボタンを押します。
「値（V)」の欄に計算した３項移動平均の値を指定します。
注意；移動平均は計算できない部分があります。現在の例では「D2」と「D61」は空白になっています。しかし同じ項目軸を使う都合上、空白であるD2からしていしてください。

「名前（N）」の欄には「３項移動平均」と入力します。
同様に5項移動平均のグラフも追加していきます。
「OK」を押します。

表３は、わが国の実質国内総生産（実質GDP）の推移を四半期ごとに示したものです。

　　　�A　　３項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。

　　　�B　　中心化４項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。

�@、�Aは例題2と同じなので�Bだけを解説します。

中心化4項移動平均は以下の公式で計算できます。

	公式	計算できないところ
中心化４項移動平均		最初と最後２つずつ計４個

中心化4項移動平均を計算してみましょう。
E列最初の「E2」、「E3」は計算できないので「E４」から計算します。
計算したい「E4」に以下の式を入力します。

＝（0.5*C2+C3+C4+C5+0.5*C6)/4

「E4」に結果が出力されたらセルの右下にマウスを移動しマウスの矢印が＋に変わったら左クリックを押しながら最後の２個前である「E95」まで移動し、左クリックを離します。
グラフは例題2と同様に作成してください。

例題１に関して以下の質問に答えなさい。
�@      １９８７年から９０年にかけて、地価・株価の高騰を中心に景気が拡大した、「バブル期」の実質経済成長率を求めなさい。
�A     1９９１年から９５年のバブル崩壊後の、実質経済成長率を求めなさい。
�B      １９９５年から９８年までの実質経済成長率を求めなさい。
�C      １９９８年から２００１年までの実質経済成長率を求めなさい。
�D　　例題１と�@から�Cを通して日本経済はどのように変化してきたかを述べなさい。





表４は２００３年８月から２００４年２月までの日経平均株価についての日次時系列データである。
�@    日経平均株価の原系列について折れ線グラフを作成しなさい。
�A    ３項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�B    ５項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�C    ７項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�D    �@から�Cまでの折れ線グラフを比較し、どのような特徴があるかを述べなさい。
�E    ２００３年７月から２００４年３月までどのような変化があったかを述べなさい。


項数が増えれば、曲線は滑らかになってきます。�@から�Cを通して滑らかになっているか確認し、特徴を述べてください。


表５は、北海道の失業率の推移を四半期ごとに示したものです。
�@      失業率の原系列について折れ線グラフを作成しなさい。
�A      ３項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�B      中心化４項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�C　　�Aのグラフと�Bのグラフでは推移を把握するためにはどちらがよいと思いますか？またその理由を書きなさい。


４半期データですから４つで１つの周期になっています。３項移動平均と４項移動平均のうち、滑らかになっているほうが推移を表すのには適しています。

第1回の講義でダウンロードした自分の関心のある企業の株価（終値、2006年1月から、週間）を課題4のワークシートにコピーした上で以下の設問を行いなさい。
�@      株価の原系列について折れ線グラフを作成しなさい。
�A      中心化４項移動平均を計算し、�@のグラフに折れ線グラフを追加しなさい。
�B      今年の株価の動向について簡単にまとめなさい。（50字以上）

�Bについては、グラフを作成した期間に上昇していたのか、下降していたのか、いつまでは上昇(下降）して、それからどのように変化していったのか、などの変化をまとめましょう。さらに、そのような変化がなぜ起こったかを考えて、まとめるとさらによいと思います。