

第5回 相関係数と散布図
![]()
表1のデータは、東京都区部における1994年1月~8月の月平均気温Xと、一世帯当たりビール消費量Yを示しています。
①散布図を描きなさい。
②表を作成して相関係数を求めなさい。
③エクセル関数を用いて相関係数を求めなさい。
④分析ツールを用いて相関係数を求めなさい。
⑤エクセル統計を用いて相関係数を求めなさい。
⑥相関係数から平均気温とビールの消費量の関係について論じなさい。
⑦⑥で論じた関係の強さから、気温とビール消費はどのような関係にあると思いますか?
![]()
②![]() 相関係数は以下の公式を用いて計算します。またΣの計算はエクセルのSUM関数を用いて計算していきます。
相関係数は以下の公式を用いて計算します。またΣの計算はエクセルのSUM関数を用いて計算していきます。
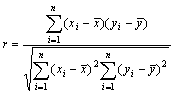
![]()
![]()
例題1のワークシートにある表を完成させて基本統計量を計算しましょう!
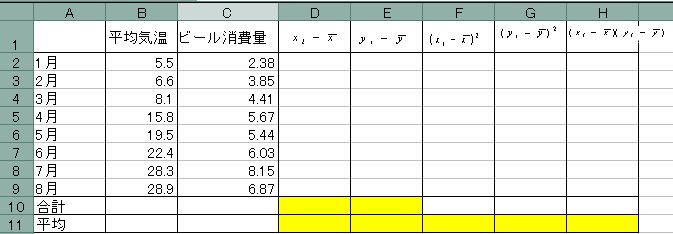
![]() まずは合計を計算します。合計の計算はSUM関数を用いましょう。
まずは合計を計算します。合計の計算はSUM関数を用いましょう。
合計を出力させたいB10のセルをクリックし、エクセルの上にある![]() マークを押します。
マークを押します。
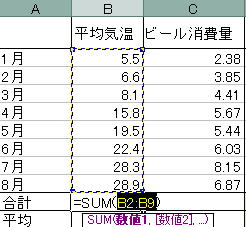
上の図のように1月から8月までが選択されていれば点線で囲まれた部分の合計が計算できます。
点線で囲まれた範囲が正しければEnterを押します。
![]() 次に平均を計算します。
次に平均を計算します。
平均=合計÷個数
で計算できます。データの個数は8個で、合計はセルB10に計算してあります。
よってセルB11に
=B10/8
と入力し、Enterを押します。
![]() C列もB列と同様に合計、平均を計算しましょう
C列もB列と同様に合計、平均を計算しましょう
![]() 次にD列の
次にD列の![]() の部分を計算します。
の部分を計算します。
B列にある数値からB11の値を引けば計算できます。よって
それぞれに
=B?-B11
となるようにします。ここでB11は必ずこの値を指定したいので絶対参照をします。
よってセルD2をクリックし、
=B2-B$11
と入力し、Enterを押します。ここで$は絶対参照をあらわしています。
ここまでできたらセルD2を「コピー」し、D3からD9まで「貼り付け」を行います。
![]() 同様にE列も計算しましょう。
同様にE列も計算しましょう。
![]() 次にF列の
次にF列の![]() の部分を計算します。
の部分を計算します。
D列にある数値を2乗すれば計算できます。2乗は^を用いて計算します。
よってセルF2をクリックし、
=D2^2
と入力し、Enterを押します。
ここまでできたらセルF2を「コピー」し、F3からF9まで「貼り付け」を行います。
![]() 最後にF列の合計をSUM関数を用いて計算します。
最後にF列の合計をSUM関数を用いて計算します。
![]() 同様にG列も計算しましょう。
同様にG列も計算しましょう。
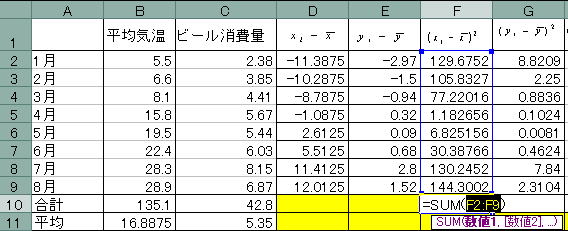
![]() 最後に次にH列の
最後に次にH列の![]() の部分を計算します。
の部分を計算します。
D列にある数値とE列にある数値を掛ければ計算できます。
よってセルH2をクリックし、
=D2*E2
と入力し、Enterを押します。
ここまでできたらセルH2を「コピー」し、H3からH9まで「貼り付け」を行います。
![]() 最後にH列の合計をSUM関数を用いて計算します。
最後にH列の合計をSUM関数を用いて計算します。
![]() これでΣの値が下記のセルに出力されています。
これでΣの値が下記のセルに出力されています。
![]() .....................F10
.....................F10
![]() ......................G10
......................G10
![]() .................H10
.................H10
これにより公式を用いて計算します。出力したいセル「C13」に
=H10/SQRT(F10*G10)
と入力します。

Enterを押せば結果が出力されます。
![]()
![]()
エクセルの組み込み関数を用いて統計量を計算してみましょう。
![]()
相関係数は以下の関数を用いて計算します。
| 相関係数 | CORREL |
![]() 相関係数を出力したいC14を左クリックして指定します。
相関係数を出力したいC14を左クリックして指定します。
![]()
![]() エクセルの上にある関数の挿入を表す
エクセルの上にある関数の挿入を表す![]() を押します。
を押します。
![]() 関数の分類は「統計」にすると候補が絞れて便利です。
関数の分類は「統計」にすると候補が絞れて便利です。
![]() 関数名の中から「CORREL」を探し、左クリックした後「OK」を押します。
関数名の中から「CORREL」を探し、左クリックした後「OK」を押します。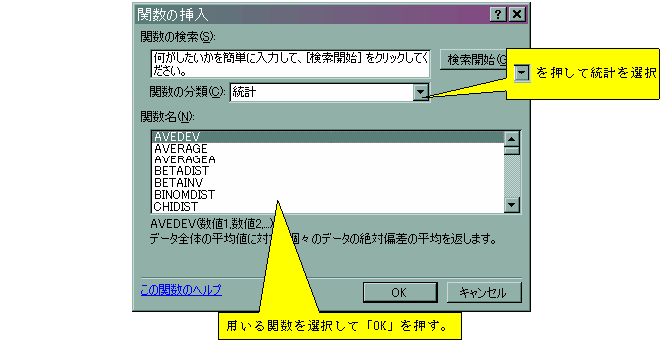
![]() 「関数の引数」ダイアログボックスが表示されたらデータの範囲を指定します。
「関数の引数」ダイアログボックスが表示されたらデータの範囲を指定します。
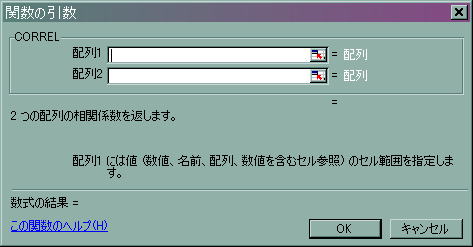
![]() 配列1の
配列1の![]() を押してXの値であるB2からB9までを左クリックを押しながら範囲を指定します。
を押してXの値であるB2からB9までを左クリックを押しながら範囲を指定します。
![]() 範囲が指定できたら再度
範囲が指定できたら再度![]() を押し、「関数の引数」ダイアログボックスに戻ります。配列1にB2:B9と入力されていることを確認します。
を押し、「関数の引数」ダイアログボックスに戻ります。配列1にB2:B9と入力されていることを確認します。
![]() 同様に配列2にはYの値であるC2からC9までを左クリックを押しながら範囲を指定します。
同様に配列2にはYの値であるC2からC9までを左クリックを押しながら範囲を指定します。
![]() 最後に「OK」を押します。
最後に「OK」を押します。
![]()
![]()
分析ツールを用いて基本統計量を出力させましょう。
![]() 「ツール」⇒「分析ツール」とし、左クリックを押し、「データ分析」ダイアログボックスを出力させます。
「ツール」⇒「分析ツール」とし、左クリックを押し、「データ分析」ダイアログボックスを出力させます。
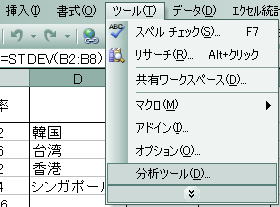

![]() 「相関」を選択し、{OK」を押して「基本統計量」ダイアログボックスを出力させる。
「相関」を選択し、{OK」を押して「基本統計量」ダイアログボックスを出力させる。

![]() 入力範囲には
入力範囲には![]() を押して範囲を指定する。
を押して範囲を指定する。
注意;
![]() 分析ツールを用いて相関係数を計算する場合は求めたいデータが隣り合っていなければなりません。もしそうなっていないワークシートであればワークシートを作成する必要があります。
分析ツールを用いて相関係数を計算する場合は求めたいデータが隣り合っていなければなりません。もしそうなっていないワークシートであればワークシートを作成する必要があります。
![]() 変数名も出力したいのでタイトルが入力されている2行目から指定する。
変数名も出力したいのでタイトルが入力されている2行目から指定する。
![]() 入力範囲は「B2]から「C9」までを指定する。
入力範囲は「B2]から「C9」までを指定する。
![]() 先頭行をラベルとして使用の欄にチェックを入れる
先頭行をラベルとして使用の欄にチェックを入れる
![]() 出力先を指定する。「出力先」にチェックを入れ
出力先を指定する。「出力先」にチェックを入れ![]() を押し、「F15」を押します。
を押し、「F15」を押します。
![]() 以上の作業を行い、上記のように設定できたら「OK」を押す。
以上の作業を行い、上記のように設定できたら「OK」を押す。

以上のように出力されているかを確認してください。
![]()
![]()
エクセル統計を用いて相関係数を計算してみましょう
![]() 「エクセル統計」⇒「基本統計量」⇒「相関行列・偏相関行列」を選択し、左クリックを押します。
「エクセル統計」⇒「基本統計量」⇒「相関行列・偏相関行列」を選択し、左クリックを押します。
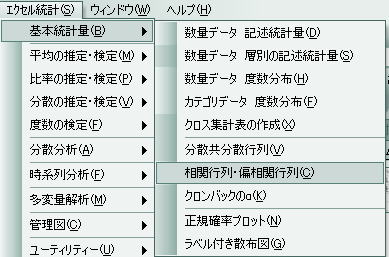
![]() 入力範囲には
入力範囲には![]() を押して範囲を指定する。
を押して範囲を指定する。
注意;
![]() エクセル統計を用いて相関係数を計算する場合は求めたいデータが隣り合っていなければなりません。もしそうなっていないワークシートであればワークシートを作成する必要があります。
エクセル統計を用いて相関係数を計算する場合は求めたいデータが隣り合っていなければなりません。もしそうなっていないワークシートであればワークシートを作成する必要があります。
![]() 変数名も出力したいのでタイトルが入力されている2行目から指定する。
変数名も出力したいのでタイトルが入力されている2行目から指定する。
![]() 入力範囲は「B2]から「C9」までを指定する。
入力範囲は「B2]から「C9」までを指定する。
![]() 以上の作業を行い、上記のように設定できたら「OK」を押す。
以上の作業を行い、上記のように設定できたら「OK」を押す。
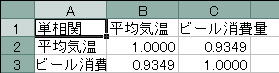
![]() 新しいワークシートに以下のように出力されているか確認してください。
新しいワークシートに以下のように出力されているか確認してください。
![]() 相関係数の判断
相関係数の判断
相関係数には以下の性質があります。
| (1)相関係数が正(プラスの値)の場合「正の相関」と呼ぶ。 (2)正の相関の場合には一方が増えればもう一方も増える。 (3)相関係数が負(マイナスの値)の場合「負の相関」と呼ぶ。 (4)負の相関の場合には一方が増えればもう一方は減る。 (5)相関係数が「+1」の場合「正の完全相関」と呼ぶ。 (6)相関係数が「-1」の場合「負の完全相関」と呼ぶ。 (7)相関係数が「0」の場合「無相関」と呼ぶ。 |
相関係数(r)の判断の仕方はいろいろとありますが、ここでは以下のように判断してみましょう。
| r>0.9の場合 | 非常に強い正の相関 |
| 0.7<r<0.9の場合 | 強い正の相関 |
| 0.3<r<0.7の場合 | 弱い正の相関 |
| -0.3<r<0.3の場合 | 関連性はない |
| -0.7<r<-0.3の場合 | 弱い負の相関 |
| -0.9<r<-0.7の場合 | 強い負の相関 |
| r<-0.9の場合 | 非常に強い負の相関 |
![]() 平均気温とビールの消費量では0.93…と得られましたからデータの関係としては上の表から
平均気温とビールの消費量では0.93…と得られましたからデータの関係としては上の表から
「平均気温とビール消費量は非常に強い正の相関がある」と判断されます。
この結果から、気温とビール消費の関係がどのようなものかわかります。特に正の相関なので、一方が大きくなればもう一方も大きくなるという関係がわかりました。ですから、「気温が高くなればビール消費量は高くなる傾向にある。よって夏場はビール消費が高くなり、冬場はビール消費が低くなることがわかる。」といえるでしょう。
これは自然な結果と思いますが皆さんはどう思いますか?
![]()
表2は家計調査における平成15年平均の勤労者世帯における都市階級・地方・都道府県庁所在市別1世帯当たり1か月間の収入と支出のうち、消費支出を10大費目別にまとめたものである。
①
費目別の消費支出について相関行列を計算しなさい。
②
食費にもっとも関係のある費目を答えなさい。
③
食費と正の相関にあって最も関係のある費目を答えなさい。
④
食費と負の相関にあって最も関係のある費目を答えなさい。
⑤
食費とまったく関係のない費目を答えなさい。
⑥
交通・通信と保健医療の費目に対して無相関の検定を行いなさい。
⑦
⑥の結果をまとめなさい。
![]()
例題1では2変量の相関係数を求めましたが、「分析ツール」や「エクセル統計」を用いれば多変量の相関係数を一括して出力させることができます。また「エクセル統計」では相関係数の出力だけではなく「相関係数の検定」、お行ってくれます。ここでは「エクセル統計」を用いて多変量のデータに対して相関係数の計算と無相関の検定を行ってみます。
![]() 例題2では10個の変数があります。これらを一括して相関係数を求めてみましょう。
例題2では10個の変数があります。これらを一括して相関係数を求めてみましょう。

![]() 「エクセル統計」⇒「基本統計量」⇒「相関行列・偏相関行列」を選択し、左クリックを押します。
「エクセル統計」⇒「基本統計量」⇒「相関行列・偏相関行列」を選択し、左クリックを押します。


![]() 入力範囲には
入力範囲には![]() を押して範囲を指定する。
を押して範囲を指定する。
注意;
![]() 変数名も出力したいのでタイトルが入力されている1行目から指定する。
変数名も出力したいのでタイトルが入力されている1行目から指定する。
![]() 入力範囲は「B1]から「K50」までを指定する。
入力範囲は「B1]から「K50」までを指定する。
![]() 検定の欄には「無相関の検定」にチェックを入れる。
検定の欄には「無相関の検定」にチェックを入れる。
![]() 以上の作業を行い、上記のように設定できたら「OK」を押す。
以上の作業を行い、上記のように設定できたら「OK」を押す。
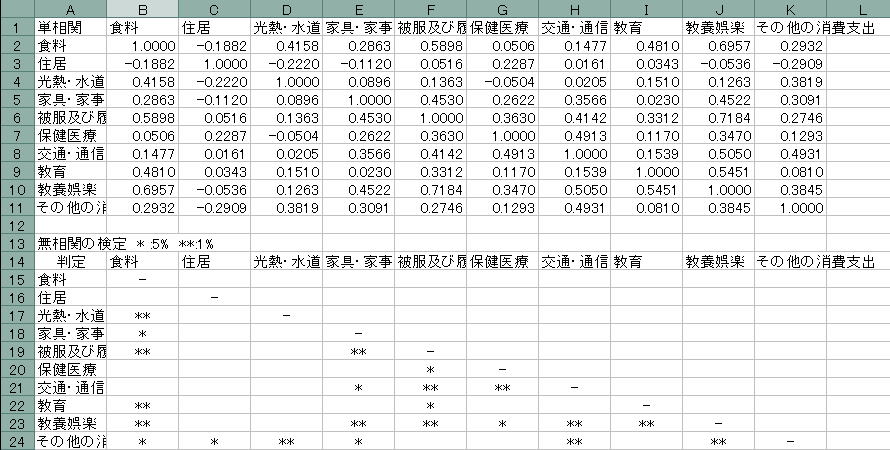
![]() 新しいワークシートに以下のように出力されているか確認してください。
新しいワークシートに以下のように出力されているか確認してください。
![]()
![]()
相関係数が行列化されているものを相関行列と呼びます。相関行列では求めたい2つの変数の相関係数は項目で交わったところに出力されています。例えば「住居」と「光熱・水道」の相関係数は2つの項目が交わった「-0.220」という値になります。
(縦と横が変わっても同じ値が出力されます)
| 単相関 | 食料 | 住居 | 光熱・水道 |
| 食料 | ↓ | ||
| 住居 | ⇒ | ⇒ | -0.220 |
| 光熱・水道 |
自分自身との関係は正の完全相関ですから値は1になっています。このように相関行列は対角部分は必ず1になります。
![]() 例題2の②から⑤までは食費との関係についての質問ですから食費となっている2列目を横に見て(あるいはB列を縦に見て)いき答えていきます。なお、食費との相関1は自分自身との関係であるため答える場合には除きます。
例題2の②から⑤までは食費との関係についての質問ですから食費となっている2列目を横に見て(あるいはB列を縦に見て)いき答えていきます。なお、食費との相関1は自分自身との関係であるため答える場合には除きます。
②
食費にもっとも関係のある費目ですからもっとも値が高い(符号は関係ない)費目を答えます。
③
食費と正の相関にあって最も関係のある費目ですから符合が正(プラス)の中で最も値が高い費目を答えます。
④
食費と負の相関にあって最も関係のある費目ですから符合が正(プラス)の中で最も値が高い費目を答えます。
⑤
食費とまったく関係のない費目ですからもっとも0に近い費目を答えます(符号は関係なし)。
答え ②教養娯楽③教養娯楽④住居⑤保健医療
![]() 例題2では無相関の検定にチェックを入れましたから、その結果も出力されます。上の例では13行目から出力されています。無相関の検定の見方は*がついているかで判断します。判定の基準は以下のとおりです。
例題2では無相関の検定にチェックを入れましたから、その結果も出力されます。上の例では13行目から出力されています。無相関の検定の見方は*がついているかで判断します。判定の基準は以下のとおりです。
| 判定 | 結果 | ||
| *がない | 有意でない | 無相関である | |
| *が1つ | * | 5%有意 | 無相関ではない |
| *が2つ | ** | 1%有意 | 無相関ではない |
⑥交通・通信と保健医療の費目に対しての検定ですから上のところで交通・通信と保健医療が交わるセル(「G21」)をみます。
(無相関の検定では下三角行列で表記されています。注意してください)
ここでG21には「**」という結果が出力されています。これから「1%有意で無相関ではない」という結果になります。
⑦ 家計調査における平成15年平均の勤労者世帯における都市階級・地方・都道府県庁所在市別1世帯当たり1か月間の収入と支出のうち、消費支出のうち、交通・通信費と保健医療費に関する無相関の検定を行ったところ、1%有意で相関があると判定された。よって交通・通信費と保健医療費には関連性がある。
![]()
表3は、わが国の実質家計可処分所得Xと実質家計最終消費支出Yを、1981年から94年までの14年間について示したものです。
①散布図を描きなさい。
②表を作成して相関係数を求めなさい。
③エクセル関数を用いて相関係数を求めなさい。
④分析ツールを用いて相関係数を求めなさい。
⑤エクセル統計を用いて相関係数を求めなさい。
⑥相関係数から実質家計可処分所得Xと実質家計最終消費支出Yの関係について論じなさい。
⑦⑥で論じた関係の強さから、所得と消費はどのような関係にあると思いますか?
![]()
例題2について以下の質問に答えなさい。
①
光熱・水道費にもっとも関係のある費目を答えなさい。
②
光熱・水道費と正の相関にあって最も関係のある費目を答えなさい。
③
光熱・水道費と負の相関にあって最も関係のある費目を答えなさい。
④
光熱・水道費とまったく関係のない費目を答えなさい。
⑤
被服および履物費と教育費の費目に対して無相関の検定を行いなさい。
⑥ ⑤の結果をまとめなさい。
![]()
課題3 表4は、2000 年の労働力調査における都道府県別の産業別1次産業、2次産業、3次産業就業者のデータである。
①
産業別就業者について相関行列を求めなさい。
②
産業別就業者割合について相関行列を求めなさい。
③
なぜ、①と②の結果は異なるのかを述べなさい。
![]()