第７回 回帰分析
表1は，わが国の実質家計可処分所得Xと実質家計最終消費支出Yを，1981年から94年までの14年間について示したものです．
①
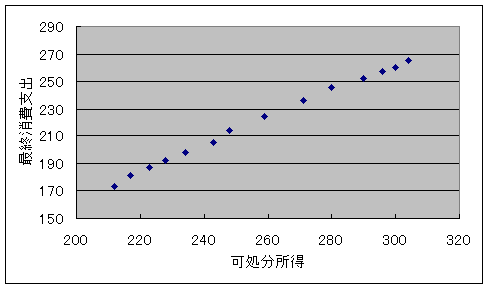
ヨコ軸にX、タテ軸にYをとり、このデータの散布図を描きなさい。
②
次のマクロ消費関数
を、OLSにより以下の方法で推定しなさい。また理論値と残差、決定係数をそれぞれの方法で出力させなさい。
(a)
表を用いた方法
(b)
分析ツールを用いた方法
(c)
エクセル統計を用いた方法
(d)
散布図からの出力
③
②で得られた回帰式を表しなさい。
④
限界消費性向を求めなさい。
⑤
②で推定したマクロ消費関数を用いて、実質家計可処分所得が
（a） ２７０兆円
（b） ３２０兆円
のときの実質家計最終消費支出をそれぞれ予測しなさい。
⑥
残差グラフを作成し、動向について論じなさい。
⑦ 決定係数
を計算し、推定されたマクロ消費関数の適合度について吟味しなさい。
① 散布図については先週行いました．各自作成してください．
詳しくは以下の作成方法をクリックしてください。
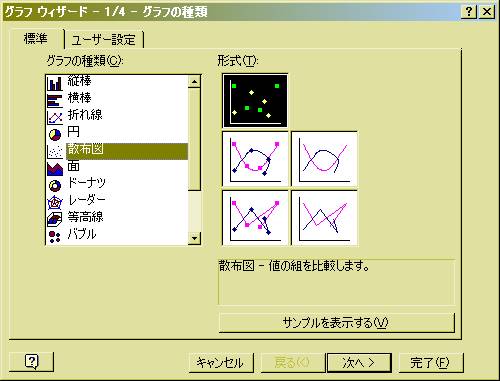
グラフウイザードの指示に従い，グラフ軸のタイトルなどを埋めてください．
また軸の書式で目盛範囲を変えると見やすいグラフが作成できます
 |
 |
（2） 方法は以下の2通りあります．それぞれのやり方を試してみましょう．なお，しっかりと分析したいのであれば分析ツールを用いた方法を行ってください．
添付ファイルの表を作成してみましょう。実際に計算過程を追うことで求め方を理解していきましょう。結果が出たら上の結果と同じか確認してください．
表の作成の仕方
(1) 合計は関数SUMを用います。
(2) 平均は関数AVARAGEを用います．
(3) D2に以下のように入力してみます。（＄を忘れずに)
(4) D列、E列はD2のセルをコピーします。
(5) F2に以下のように入力します。
(6) F列G列はF2のセルをコピーします。
(7) H2に以下のように入力し，H列にコピーします。
(8) F16、G16、H16のセルに関数SUMを用いて合計を出します．
| A | B | C | D | E | F | G | H | |
| 2 | 年 | Ｘ | Ｙ | x-bar(x) | y-bar(y) | (x-bar(x))^2 | (y-bar(y))^2 | (x-bar(x))(y-bar(y)) |
| 3 | 1981 | 212 | 173 | =B2-B$17 | =D2^2 | =D2*E2 | ||
| 4 | 1982 | 217 | 181 | |||||
| 5 | 1983 | 223 | 187 | |||||
| 6 | 1984 | 228 | 192 | |||||
| 7 | 1985 | 234 | 198 | |||||
| 8 | 1986 | 243 | 205 | |||||
| 9 | 1987 | 248 | 214 | |||||
| 10 | 1988 | 259 | 225 | |||||
| 11 | 1989 | 271 | 236 | |||||
| 12 | 1990 | 280 | 246 | |||||
| 13 | 1991 | 290 | 252 | |||||
| 14 | 1992 | 296 | 257 | |||||
| 15 | 1993 | 300 | 260 | |||||
| 16 | 1994 | 304 | 265 | |||||
| 17 | 合計 | = | 関数SUM | 関数SUM | 関数SUM | |||
| 18 | 平均 |
まず傾きと切片を求めてみましょう。結果を返すB21とB22に以下のように入力してみます。
| A | B | |
| 21 | 傾き | =H16/F16 |
| 22 | 切片 | =C17-B21*B17 |
| 23 | 決定係数 | |
| 24 | 相関係数 | |
| 25 | 相関係数^2 |
次に残差を計算します。
(1) I3,J3、K3のセルに以下のように入力してみます．
(2) I3,J3、K3のセルをコピーし，16列まで貼り付けます．
関数SUMを用いてセルK17に合計を計算します。
| I | J | K | |
| 2 | 予測値 | 残差 | 残差^2 |
| 3 | =B3*$B$21+$B$22 | =I3-C3 | =J3^2 |
| 4 |
公式に当てはめて決定係数を計算します．
また関数CORRELを用いて相関係数を計算してみます．
| A | B | |
| 21 | 傾き | =H16/F16 |
| 22 | 切片 | =C17-B21*B17 |
| 23 | 決定係数 | =1-K17/G17 |
| 24 | 相関係数 | |
| 25 | 相関係数^2 |
手順１
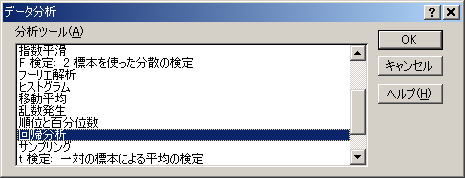
まずメニューから「ツール」⇒「分析ツール（D)」を選択し，データ分析画面を出力させます。
手順2
回帰分析を選択して「OK」を押します．
 |
 |
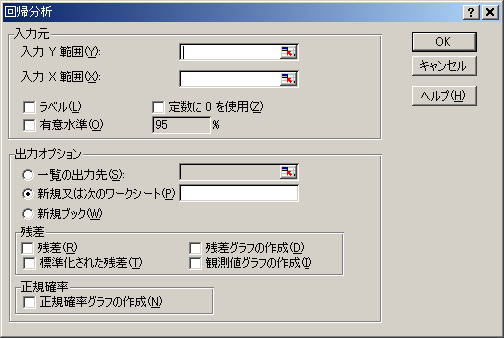手順３
「Y入力範囲」には変数Yのデータ範囲を指定し、「X入力範囲」には変数Xのデータ範囲を指定します。今は
Y:実質家計可処分所得
X:実質家計最終消費支出
ですから添付データのセルC3からC17をマウスで選択します。同様にXも選択してみましょう。
今回はすべてにチェックしておきましょう。最後に「OK」を押します．
 |
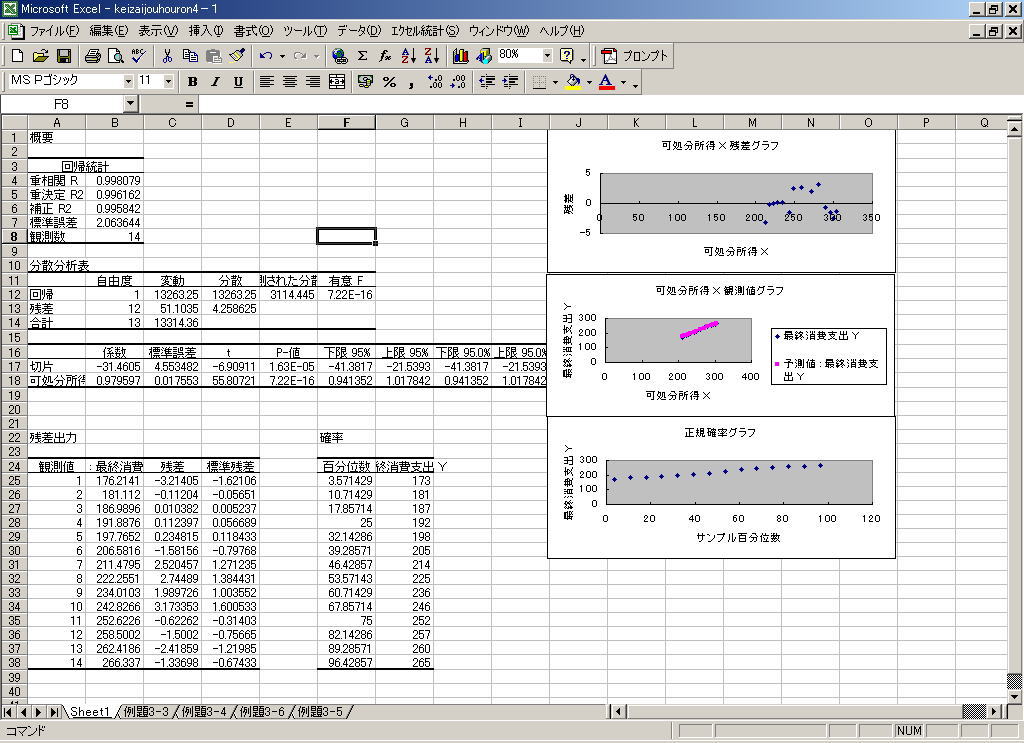得られた結果の出力画面のうち以下の項目に注目します．
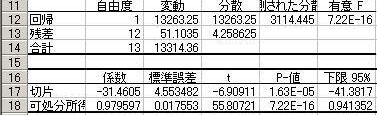
17，18行目に表示されている切片，可処分所得の係数にあたるところが回帰直線の切片と傾きになります．よって答えは
Y=0.979597X-31.4605
となります．
これでできあがり
セルB23の値とB25の値が一致しているか確認してください。
また、B21からB23の値が分析ツールの値と一致しているかも確認してください。
手順１
まずメニューから「エクセル統計」⇒「多変量解析」⇒「重回帰分析」を選択し，ダイアログボックスを出力させます。
手順２
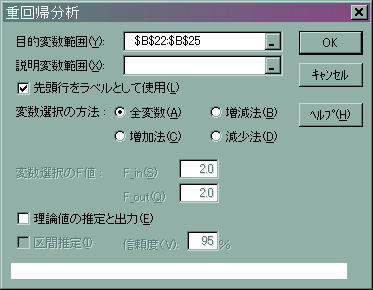
「目的変数範囲」には変数Yのデータ範囲を指定し、「説明変数範囲」には変数Xのデータ範囲を指定します。今は
目的変数:実質家計可処分所得
説明変数:実質家計最終消費支出
ですから添付データのセルC２からC17をマウスで選択します。同様にXも選択してみましょう。
注意 エクセル統計では先頭行をラベルとして使用することがデフォルトになっています。何回も注意してますね!
手順３
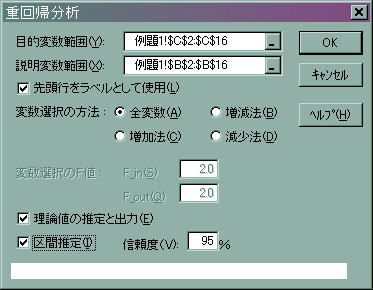
変数選択の方法は全変数にチェックし、すべてにチェックを入れます。
最後に「OK」を押します．
 |
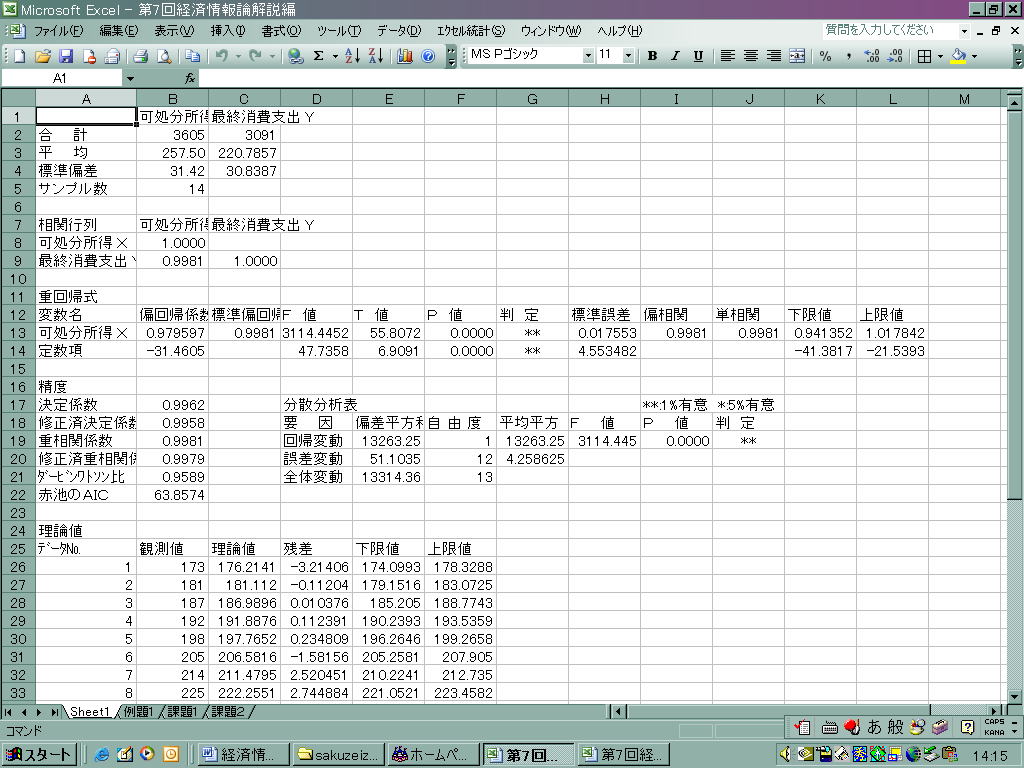得られた結果の出力画面のうち以下の項目に注目します．
1３，1４行目に表示されている可処分所得の係数、定数項にあたるところが回帰直線の傾きと切片になります．よって答えは
Y=0.979597X-31.4605
となります．
また、精度や理論値などから、理論値、残差、決定係数を読み取っていきます。
これでできあがり
手順1
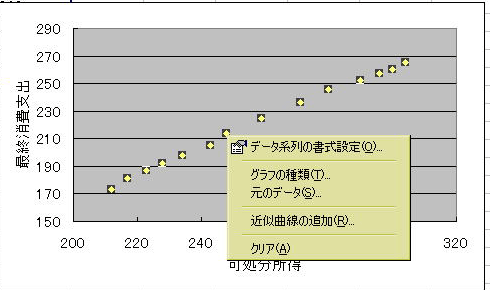
先週行った方法で近似曲線を作成します。グラフで系列をチェックし、「右クリック」⇒「近似曲線の選択」で[近似曲線の追加]ウインドを開きます。
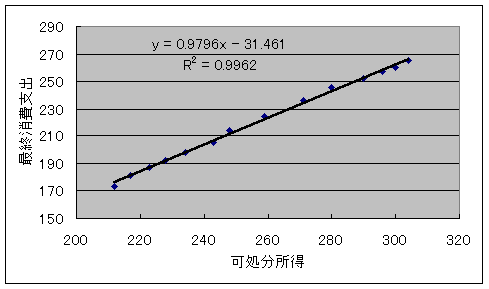
種類に線形近似になっているか確認し、系列で必要なところをチェックします．すると近似曲線とともに回帰式，決定係数が表示されます．
 |
 |
 |
これでできあがり
③ ②で求めた傾きがα、切片がβを表しています。よって回帰式は
Y=0.979597X-31.4605
となります。
④限界消費性向とはαの値をいいます。よって
限界性向は0.979597
となります。
⑤ （2）から回帰式は
Y=0.979597X-31.4605
と得られました．この回帰式のXに代入すれば計算できます。
(a) いま，Xが２７０兆円のときのYの値を計算したいのですから
0.979597×２７０-31.4605
を計算すればよいことになります．結果を返すセルに回帰係数を参照させて
=B２１*２７０+B２２
（セルB２１には可処分所得の傾きが入っていてセルB２２には切片の係数が入っています）
と入力すれば結果として233.0306768が返されます．よって予測値は
約２３３兆円
と答えればいいのです．
(ｂ) 同様に，Xが３２０兆円のときのYの値を計算したいのですから
0.979597×３２０-31.4605
を計算すればよいことになります．結果を返すセルに回帰係数を参照させて
=B２１*３２０+B２２
（セルB２１には可処分所得の傾きが入っていてセルB２２には切片の係数が入っています）
と入力すれば結果として282.0105271が返されます．よって予測値は
約２８２兆円
と答えればいいのです．
⑥ 分析ツールの結果画面からグラフを作成してみましょう。
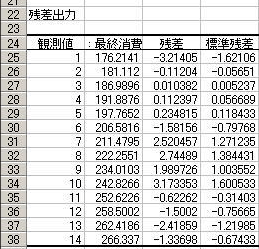
残差のグラフとして折れ線グラフを作成してみます。
ここで項目軸にはそれぞれの年を指定しました。
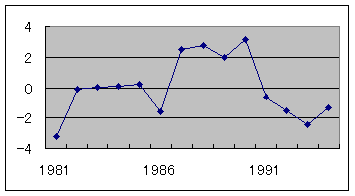
⑦ グラフから求める場合には近似曲線のプロンプトのオプションでR-2乗値を計算にチェックを入れれば出力されます．
分析ツールの結果画面では
からわかります．ここで一般的に用いられているのは重決定係数R2の値です．
よって答えは0.996162となります．
決定係数の値の吟味は様々ですが本講義では以下のように判断すればよいでしょう．
| 決定係数の値 | 判断 |
| 0.9以上 | 非常に当てはまりがよい |
| 0.7以上0.9未満 | 当てはまりがよい |
| 0.5以上0.7未満 | あまり当てはまりはよくない |
| 0.5未満 | 当てはまりは悪い |
今回は0.996と高い値が出ましたから非常に当てはまりがよいとなります．
表２は、東証第１部上場の医薬品メーカー３４社の売上高Xと経常利益Yを、１９９６年３月期決算から掲げたものです。両者の関係は、わが国の企業経営において強く意識される財務要因のひとつです。
1 単純回帰モデルを、OLSにより以下の方法で推定しなさい。また理論値と残差を出力させなさい。(a)
表を用いた方法
(b)
分析ツールを用いた方法
(c)
エクセル統計を用いた方法
(d)
散布図からの出力
２ 決定係数R２と相関係数を計算しなさい。
３ 収益力が高い3社を挙げなさい。
４ 収益力の低い3社を挙げなさい。
収益力が高い会社と低い会社とは、理論的な利益よりも多く利益を上げている会社が収益力の高い会社、理論的な利益よりも実際の利益が少ない会社が収益力の悪い会社です。つまり、残差が高い会社ほど収益力がよく、残差が低いほど収益力が悪いと判断できるのです。
表２は家計調査における平成15年平均の勤労者世帯における都市階級・地方・都道府県庁所在市別１世帯当たり１か月間の収入と支出のうち、可処分所得（X）と消費支出（Y）を都道府県別にまとめたものである。
①
ヨコ軸にX、タテ軸にYをとり、このデータの散布図を描きなさい。
②
次のマクロ消費関数
を、OLSにより以下の方法で推定しなさい。また理論値と残差をそれぞれの方法で出力させなさい。
③
限界消費性向を求めなさい。
④
例題1では時系列データ（マクロデータ）について分析を行いました。限界消費性向を比較して論じなさい。
⑤
②で推定したマクロ消費関数を用いて、北海道の消費支出の理論値と残差を出力し、北海道の消費について吟味しなさい。
⑥
決定係数を計算し、推定されたマクロ消費関数の適合度について吟味しなさい。
表4は日本の企業のうち、2004年度における広告宣伝費が多い上位100社の広告宣伝費、売上高、経常利益を表したものです。
① 目的変数を売上高、説明変数を広告宣伝費として回帰分析を行いなさい。
② 目的変数を経常利益、説明変数を広告宣伝費として回帰分析を行いなさい。
③ ①と②を比較して、適合度が高いものはどちらかを答えなさい。さらに、なぜそのような結果が得られるのかを考えて理由をまとめなさい。
以下は①の結果から答えなさい。
④ 回帰分析で得られた傾き（偏回帰係数）は何を表しているかを答えなさい。
⑤ 広告効果が高い企業上位3社と、低い企業上位3社を挙げなさい。
⑥ 広告効果が高い業種、低い業種を上げ、なぜそのような結果になるのかを考えなさい。
③； 商品の宣伝は売り上げ増を期待して行います。よって宣伝をすれば売り上げは高くなるでしょう。利益とは売上から支出を引いたものなので、売上が高くなったとしてもその分支出が多くなれば利益は高くはなりません。
④； 偏回帰係数はXが1単位（単位が百万円ならば100万円）増えたときのYの増加分を表しています。ここで行った分析結果から何が増えた場合の増加分なのかを考えて答えてください。ちなみに
例題１で同様の問題があるとしたら、「実質家計可処分所得が1兆円増加した場合の実質家計最終消費支出の増加分」と答えればよいでしょう。
⑤； 「広告効果が高い」→「広告費に対して売上が高い」→「残差が大きい」として考えましょう。実際には広告効果以外にも売上には影響しているので、一概にはこのようなことが言えませんが。。。。。
⑥； 残差が大きい企業で特に目立つ業種、小さい企業で目立つ業種を挙げて、なぜこのような結果が得られたのかを考えて答えましょう。
広告効果の高い業種は△△であった。これは.................のためだと思われる。一方、広告効果の低い業種は□□であった。これは.................のためだと思われる。